Lập Trình Không Khó

Học lập trình theo cách riêng của bạn!

Bạn đang ở:Trang chủ / CTDL và Giải thuật / Cấu trúc dữ liệu / Cây tìm kiếm nhị phân – Binary search tree

Cây tìm kiếm nhị phân – Binary search tree

by Để lại bình luận

Trong bài viết này, chúng ta sẽ tiếp tục tìm hiểu về cấu trúc dữ liệu Cây, và cụ thể là cây tìm kiếm nhị phân. Đây là một cấu trúc dữ liệu được dùng khá phổ biến và có tính ứng dụng cao. Hãy cùng Nguyễn Văn Hiếu tìm hiểu và cài đặt cây tìm kiếm nhị phân sử dụng ngôn ngữ C/C++ nhé.

1. Lý thuyết về cây tìm kiếm nhị phân

Cây tìm kiếm nhị phân(TA: Binary Search Tree – viết tắt: BST) – là một cây nhị phân và có thêm các ràng buộc sau đây:

  1. Giá trị của tất cả các Node ở cây con bên trái phải <= giá trị của Node gốc.
  2. Giá trị của tất cả các Node ở cây con bên phải phải > giá trị của Node gốc.
  3. Tất cả các cây con(bao gồm bên trái và phải) cũng đều phải đảm bảo 2 tính chất trên.
Nhận biết cây tìm kiếm nhị phân
Nhận biết cây tìm kiếm nhị phân. Hình thứ 2 không phải BST do vi phạm ràng buộc số 2

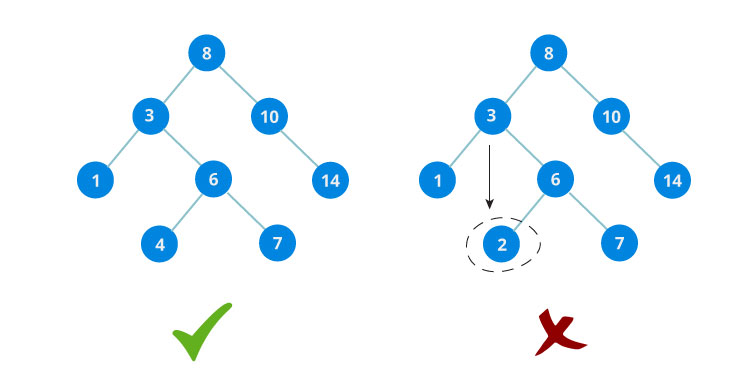
Cây tìm kiếm nhị phân là một cấu trúc dữ liệu hiệu quả cho phép chúng ta xây dựng nên một danh sách mà dữ liệu trên đó được sắp xếp:

  • Nó được gọi là cây nhị phân vì mỗi Node của cây chỉ có tối đa hai con
  • Nó được gọi là cây tìm kiếm nhị phân vì nó có thể được sử dụng để tìm kiếm sự hiện diện của một phần tử trong thời gian O(log (n)).

2. Cài đặt cây BST

Sau đây, tôi sẽ cùng các bạn đi cài đặt cây tìm kiếm nhị phân sử dụng danh sách liên kết. Do đó, cái bạn cần lưu giữ là Node root của cây mà thôi. Có được root chúng ta có thể duyệt qua mọi phần tử của cây.

Đầu tiên, chúng ta sẽ định nghĩa kiểu dữ liệu cho các Node của cây:

typedef struct Node
{
    int data;
    Node* left;
    Node* right;
} node_t;

Tiếp theo, chúng ta sẽ triển khai code cho tức chức năng của cây BST. Chúng ta sẽ sử dụng đệ quy rất nhiều trong các chức năng này. Bạn có thể tự tìm hiểu cách viết khử đệ quy nhé.

2.1. Hàm giải phóng dữ liệu

Chúng ta sẽ sử dụng hàm này khi muốn xóa một cây con hoặc toàn bộ cây bằng cách cung cấp Node root của cây muốn xóa. Việc giải phóng được thực hiện theo trình tự:

  1. Gọi đệ quy xóa cây con bên trái
  2. Gọi đệ quy xóa cây con bên phải
  3. Giải phóng vùng nhớ cho con trỏ hiện tại
void Free( node_t* root )
{
    if ( root == NULL )
        return;
    Free( root->left );
    Free( root->right );
    free( root );
}

2.2. Hàm điều hướng của cây

2 hàm dưới đây sẽ phục vụ chúng ta trong quá trình Insert(thêm phần tử vào cây) và Tìm kiếm trên cây tìm kiếm nhị phân.

Nếu bạn cho phép cây BST có giá trị trùng lặp, hãy lưu ý hàm LeftOf nhé. Ở đây tôi sẽ không cho phép thêm phần tử đã có trên cây(bỏ qua trùng lặp giá trị).

int LeftOf( const int value, const node_t* root )
{
    // Nếu bạn muốn cây BST cho phép giá trị trùng lặp, hãy sử dụng dòng code thứ 2
    return value < root->data;
//    return value <= root->data;
}

int RightOf( const int value, const node_t* root )
{
    return value > root->data;
}

2.3. Thêm phần tử vào BST

Việc thêm 1 phần tử vào cây nhị phân tìm kiếm vẫn phải đảm bảo được các ràng buộc của một BST đã trình bày ở trên. Như vậy, bạn cần phải tìm kiếm vị trí thích hợp trong BST để lưu giữ nó.

Nếu bạn để ý, bạn sẽ nhận ra vị trí của các Node được thêm vào sẽ luôn Node lá(không có Child nào hết). Như vậy, tại vị trí đó trước khi các Node mới tới ở thì nó là NULL. Ta có quy trình như sau:

  1. Nếu Node hiện tại = NULL, đó là vị trí cần thêm. Thêm vào BST và kết thúc
  2. Nếu giá trị cần thêm < giá trị root hiện tại, gọi đệ quy Insert vào cây con bên trái
  3. Nếu giá trị cần thêm > giá trị root hiện tại, gọi đệ quy Insert vào cây con bên phải.
node_t* Insert( node_t* root, const int value )
{
    if ( root == NULL )
    {
        node_t* node = (node_t*)malloc( sizeof( node_t ) );
        node->left = NULL;
        node->right = NULL;
        node->data = value;
        return node;
    }
    if ( LeftOf( value, root ) )
        root->left = Insert( root->left, value );
    else if ( RightOf( value, root ) )
        root->right = Insert( root->right, value );
    return root;
}

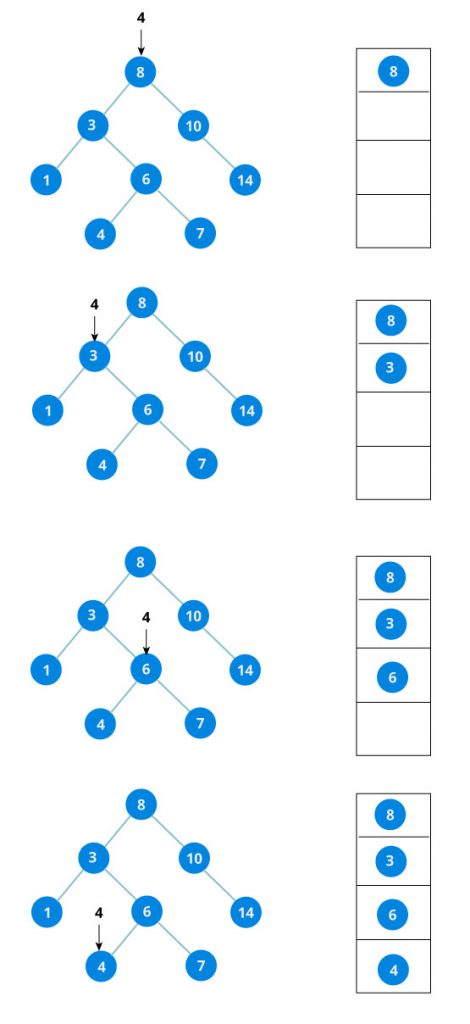
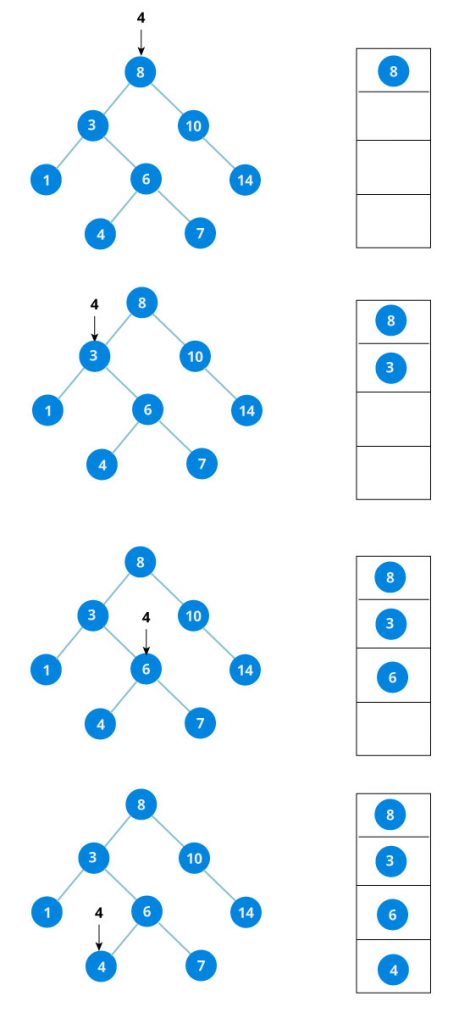
Hãy xem hình ảnh mô phỏng việc thêm giá trị 4 vào BST dưới đây:

Thêm Node vào cây tìm kiếm nhị phân

2.4. Tìm kiếm trên BST

Việc tìm kiếm cũng tương tự như việc thêm phần tử vào BST. Ta có quy trình như sau:

  1. Nếu Node hiện tại có giá trị = giá trị cần tìm, trả về true và kết thúc.
  2. Nếu Node hiện tại có giá trị > giá trị cần tìm, gọi đệ quy tìm ở cây con bên trái.
  3. Nếu Node hiện tại có giá trị < giá trị cần tìm, gọi đệ quy tìm ở cây con bên phải
  4. Nếu tìm đến hết cây(Node đó = NULL) mà không xảy ra (1), trả về false và kết thúc.
bool Search( const node_t* root, int value )
{
    if ( root == NULL )
        return false;
    if(root->data == value){
        return true;
    }else if ( LeftOf( value, root ) ){
        return Search( root->left, value );
    }else if( RightOf( value, root ) ){
        return Search( root->right, value );
    }
}

Chúng ta sẽ quan sát cách BST tìm kiếm giá trị 4 trong hình ảnh dưới đây:

Tìm kiếm trên cây tìm kiếm nhị phân

2.5. Lấy giá trị con trái nhất

Rất đơi giản, duyệt theo con trỏ trỏ đến cây con bên trái tới chừng nào không còn con bên trái nữa thì đó là con trái nhất rồi.

Hàm này sẽ được chúng ta sử dụng trong việc xóa một Node có giá trị chỉ định trên BST ở mục tiếp theo.

int LeftMostValue( const node_t* root )
{
    while ( root->left != NULL )
        root = root->left;
    return root->data;
}

Hình ảnh dưới đây mô phỏng hàm LestMostChild hoạt động:

Left most child
Con trái nhất của Node root(15) là 8; Con trái nhất của Node root(20) là 16

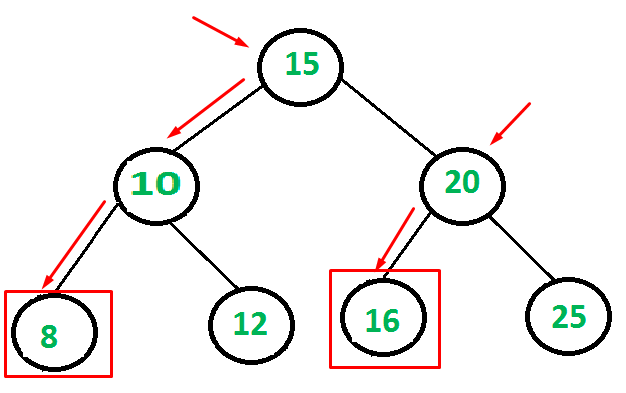
Vậy chúng ta có cần hàm RightMostChild không? Câu trả lời là có. Tuy nhiên, bạn có thể tận dùng hàm LeftMostChild này, chẳng hạn: Số 25 là right most child của root(15) có thể tính bằng LeftMostChild(root->right->right).

2.6. Xóa Node trong BST

Việc xóa Node trong BST có lẽ là phức tạp nhất trong các chức năng của cây tìm kiếm nhị phân. Nếu Node bạn cần xóa là Node lá thì việc xóa rất đơn giản. Cái khó ở chỗ xóa một Node ở trung gian, khi đó, bạn phải tìm cách xóa và nối lại mà vẫn đảm bảo cây mới vẫn là BST. Chúng ta sẽ xem xét từng trường hợp trước khi code nhé:

1. Node cần xóa là Node lá(không có child nào cả)

Giả sử ta cần xóa 20 trong hình dưới đây, đơn giản là chỉ cần giải phóng ô nhớ đó.

              50                            50
           /              delete(20)      /   
          30      70       --------->    30     70 
         /      /                           /   
       20   40  60   80                   40  60   80

2. Node cần xóa có 1 child

Trong trường hợp này, Node bị xóa sẽ được giải phóng và cây con duy nhất của Node bị xóa sẽ được liên kết trực tiếp với cha của Node bị xóa.

              50                            50
           /              delete(30)      /   
          30      70       --------->    40     70 
                /                            /   
            40  60   80                       60   80

3. Node cần xóa có đủ 2 child

Xóa node có 2 con trong BST
Giả sử cần xóa Node khoanh đỏ. Khi đó, ta cần tìm Node thế thân cho Node đỏ này, đó là Node LeftMostChild của cây con bên phải của Node đỏ(72) = Node khoanh màu xanh(54) . Sau đó, gọi đệ quy Xóa Node màu xanh. Khi đó Node cần xóa sẽ quay trở về trường hợp 1 hoặc 2(Trong ảnh này là trường hợp 2 – có 1 child).

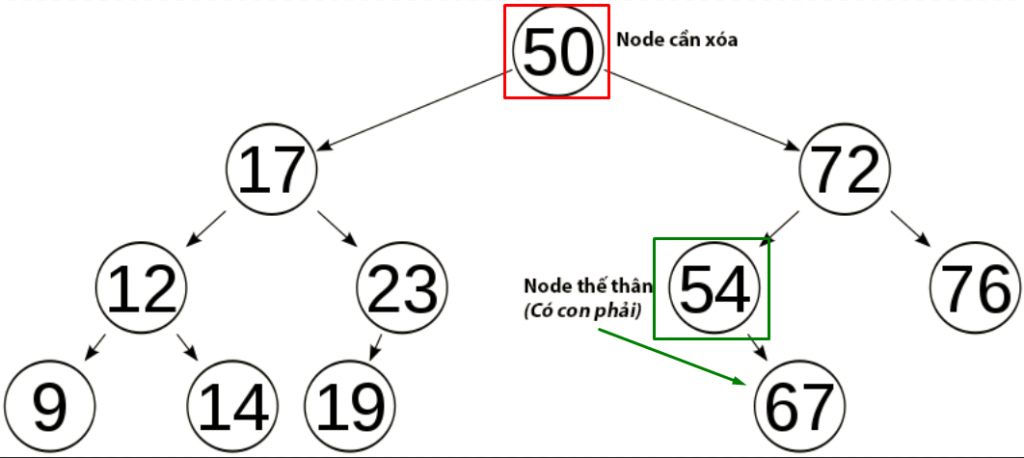
Đây là trường hợp nan giải nhất, nhưng chúng ta vẫn có cách làm như sau:

  1. Tìm Node của con trái nhất(giả sử nó là leftmost) của cây con bên phải của Node cần xóa.
  2. Cập nhật giá trị của Node cần xóa = giá trị của Node leftmost.
  3. Gọi đệ quy hàm Delete xóa Node leftmost khỏi BST.

Giải thích:

  • Khi muốn xóa Node có 2 con, ta cần tìm Node nào đó trong BST thỏa mãn tính chất lớn hơn lớn hơn tất cả các con bên trái và nhỏ hơn tất cả các con bên phái -> Node đó chính là LeftMostChild của con bên phải của Node cần xóa.
  • Ta chỉ cần sửa giá trị của Node cần xóa, không cần xóa Node đó làm gì. Thay vào đó, xóa Node bị thế thân(LeftMostChild của con bên phải của Node cần xóa).
node_t* Delete( node_t* root, int value )
{
    if ( root == NULL )
        return root;
    if ( LeftOf( value, root ) )
        root->left = Delete( root->left, value );
    else if ( RightOf( value, root ) )
        root->right = Delete( root->right, value );
    else
    {
        // root->data == value, delete this node
        if ( root->left == NULL )
        {
            node_t* newRoot = root->right;
            free( root );
            return newRoot;
        }
        if ( root->right == NULL )
        {
            node_t* newRoot = root->left;
            free( root );
            return newRoot;
        }
        root->data = LeftMostValue( root->right );
        root->right = Delete( root->right, root->data );
    }
    return root;
}

3. Duyệt cây tìm kiếm nhị phân

Ở mục này mình sẽ trình bày về 3 cách duyệt cây tìm kiếm nhị phân. Chúng ta sẽ đi vào chi tiết từng cách nhé. Thứ tự duyệt được đặt tên phụ thuộc vào vị trí của Node root trong quá trình duyệt:

  • PreOrder: Node -> Left -> Right
  • InOrder: Left -> Node -> Right
  • PostOrder: Left -> Right -> Node
  • Thực ra 3 phần tử Left, Right, Node có tất cả 6 hoán vị cơ. Còn 3 cái nữa các bạn tự cài nhé.

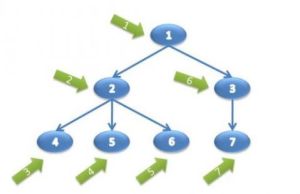
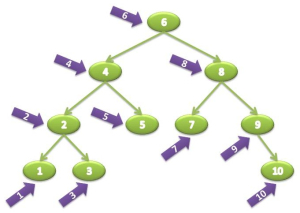
3.1. Duyệt PreOrder

Quy trình duyệt PreOrder sẽ thực hiện theo thứ tự Node -> Left -> Right, cụ thể như sau:

  1. Ghé thăm Node root
  2. Gọi đệ quy duyệt qua cây con bên trái
  3. Gọi đệ quy duyệt qua cây con bên phải
Duyệt pre_order BTS
Thứ tự duyệt pre_order trên BTS
void PreOrder(node_t* root){
    if(root != NULL)
    {
        printf("%d ", root->data);
        PreOrder(root->left);
        PreOrder(root->right);
    }
}

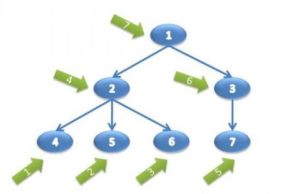
3.2. Duyệt InOrder

Quy trình duyệt PreOrder sẽ thực hiện theo thứ tự Left-> Node -> Right, cụ thể như sau:

  1. Gọi đệ quy duyệt qua cây con bên trái
  2. Ghé thăm Node root
  3. Gọi đệ quy duyệt qua cây con bên phải
Thứ tự duyệt in_order trên BTS
Thứ tự duyệt in_order trên BTS
void InOrder(node_t* root){
    if(root != NULL)
    {
        InOrder(root->left);
        printf("%d ", root->data);
        InOrder(root->right);
    }
}

3.1. Duyệt PostOrder

Quy trình duyệt PreOrder sẽ thực hiện theo thứ tự Left -> Right -> Node, cụ thể như sau:

  1. Gọi đệ quy duyệt qua cây con bên trái
  2. Gọi đệ quy duyệt qua cây con bên phải
  3. Ghé thăm Node root
Duyệt post_order trên BTS
Duyệt post_order trên BTS
void PostOrder(node_t* root){
    if(root != NULL)
    {
        PostOrder(root->left);
        PostOrder(root->right);
        printf("%d ", root->data);
    }
}

4. Code đầy đủ cây tìm kiếm nhị phân

#include <stdio.h>
#include <stdlib.h>

typedef struct Node
{
    int data;
    Node* left;
    Node* right;
} node_t;



void Free( node_t* root )
{
    if ( root == NULL )
        return;

    Free( root->left );
    Free( root->right );
    free( root );
}

int LeftOf( const int value, const node_t* root )
{
    // Nếu bạn muốn cây BST cho phép giá trị trùng lặp, hãy sử dụng dòng code thứ 2
    return value < root->data;
//    return value <= root->data;
}

int RightOf( const int value, const node_t* root )
{
    return value > root->data;
}

node_t* Insert( node_t* root, const int value )
{
    if ( root == NULL )
    {
        node_t* node = (node_t*)malloc( sizeof( node_t ) );
        node->left = NULL;
        node->right = NULL;
        node->data = value;
        return node;
    }
    if ( LeftOf( value, root ) )
        root->left = Insert( root->left, value );
    else if ( RightOf( value, root ) )
        root->right = Insert( root->right, value );
    return root;
}

bool Search( const node_t* root, int value )
{
    if ( root == NULL )
        return false;
    if(root->data == value){
        return true;
    }else if ( LeftOf( value, root ) ){
        return Search( root->left, value );
    }else if( RightOf( value, root ) ){
        return Search( root->right, value );
    }
}

int LeftMostValue( const node_t* root )
{
    while ( root->left != NULL )
        root = root->left;
    return root->data;
}

node_t* Delete( node_t* root, int value )
{
    if ( root == NULL )
        return root;
    if ( LeftOf( value, root ) )
        root->left = Delete( root->left, value );
    else if ( RightOf( value, root ) )
        root->right = Delete( root->right, value );
    else
    {
        // root->data == value, delete this node
        if ( root->left == NULL )
        {
            node_t* newRoot = root->right;
            free( root );
            return newRoot;
        }
        if ( root->right == NULL )
        {
            node_t* newRoot = root->left;
            free( root );
            return newRoot;
        }
        root->data = LeftMostValue( root->right );
        root->right = Delete( root->right, root->data );
    }
    return root;
}

void PreOrder(node_t* root){
    if(root != NULL)
    {
        printf("%d ", root->data);
        PreOrder(root->left);
        PreOrder(root->right);
    }
}

void InOrder(node_t* root){
    if(root != NULL)
    {
        InOrder(root->left);
        printf("%d ", root->data);
        InOrder(root->right);
    }
}

void PostOrder(node_t* root){
    if(root != NULL)
    {
        PostOrder(root->left);
        PostOrder(root->right);
        printf("%d ", root->data);
    }
}


int main()
{
    node_t* root = NULL;

    root = Insert( root, 25 );
    root = Insert( root, 15 );
    root = Insert( root, 50 );
    root = Insert( root, 10 );
    root = Insert( root, 22 );
    root = Insert( root, 35 );
    root = Insert( root, 70 );
    root = Insert( root, 4 );
    root = Insert( root, 12 );
    root = Insert( root, 18 );
    root = Insert( root, 24 );
    root = Insert( root, 31 );
    root = Insert( root, 44 );
    root = Insert( root, 66 );
    root = Insert( root, 90 );
    printf("nDuyet preorder : ");
    PreOrder(root);
    printf("nDuyet inorder  : ");
    InOrder(root);
    printf("nDuyet postorder:");
    PostOrder(root);

    printf("n==Thu them phan tu 15 vao BTS==n");
    Insert(root, 15);
    printf("nDuyet preorder : ");
    PreOrder(root);
    printf("nDuyet inorder  : ");
    InOrder(root);
    printf("nDuyet postorder:");
    PostOrder(root);


    printf("n==Thu xoa phan tu 50 khoi BTS==n");
    Delete(root, 50);
    printf("nDuyet preorder : ");
    PreOrder(root);
    printf("nDuyet inorder  : ");
    InOrder(root);
    printf("nDuyet postorder:");
    PostOrder(root);




    Free( root );
    root = NULL;
    return 0;
}

Trong hàm main tôi đã cài đặt BTS cho cây nhị phân sau:

Cây tìm kiếm nhị phân - Binary search tree
Cây nhị phân tìm kiếm được sử dụng trong source code

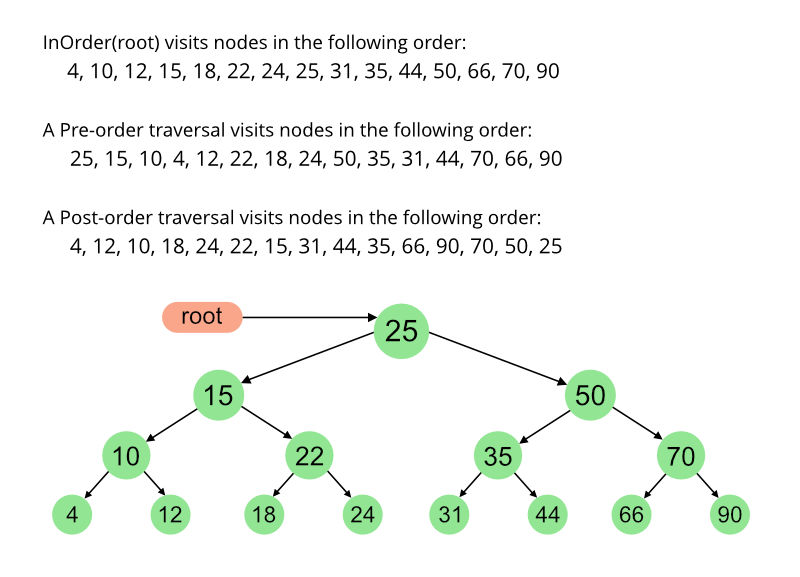
Nhờ các bạn kiểm tra kết quả chạy của code:

Duyet preorder : 25 15 10 4 12 22 18 24 50 35 31 44 70 66 90
Duyet inorder  : 4 10 12 15 18 22 24 25 31 35 44 50 66 70 90
Duyet postorder:4 12 10 18 24 22 15 31 44 35 66 90 70 50 25
==Thu them phan tu 15 vao BTS==

Duyet preorder : 25 15 10 4 12 22 18 24 50 35 31 44 70 66 90
Duyet inorder  : 4 10 12 15 18 22 24 25 31 35 44 50 66 70 90
Duyet postorder:4 12 10 18 24 22 15 31 44 35 66 90 70 50 25
==Thu xoa phan tu 50 khoi BTS==

Duyet preorder : 25 15 10 4 12 22 18 24 66 35 31 44 70 90
Duyet inorder  : 4 10 12 15 18 22 24 25 31 35 44 66 70 90
Duyet postorder:4 12 10 18 24 22 15 31 44 35 90 70 66 25
Process returned 0 (0x0)   execution time : 0.047 s
Press any key to continue.

5. Bài tập thực hành

  • https://vn.spoj.com/problems/NKTREE/
  • http://ntucoder.net/Problem/List?ThemeID=17
  • https://www.hackerearth.com/practice/data-structures/trees/binary-search-tree/practice-problems/
5/5 - (1 bình chọn)

Bài viết liên quan

Học lập trình cho người mới bắt đầu
Học lập trình online với mức giá ưu đãi
Bài tập Cấu trúc dữ liệu và Giải thuật
Bài tập cấu trúc dữ liệu và giải thuật tổng hợp
Cây nhị phân – Binary Tree

Reader Interactions

Để lại một bình luận

Email của bạn sẽ không được hiển thị công khai. Các trường bắt buộc được đánh dấu *

DMCA.com Protection Status