Thuật toán Prim (tiếng anh: Prim’s algorithm) là một thuật toán tham lam được dùng để tìm cây khung nhỏ nhất (Minimum Spanning Tree – MST) của một đồ thị liên thông có trọng số. Thuật toán được tìm ra vào năm 1975 và được đặt tên theo nhà nghiên cứu khoa học máy tính Robert C. Prim.
Một số thuật ngữ liên quan:
- Spanning Tree : là cây khung của đồ thị liên thông và vô hướng, (Cho nên thuật toán này chỉ sử dụng cho đồ thị vô hướng).
- Minimum Spanning Tree : là cây khung nhỏ nhất, (Có tổng trọng số của các cạnh là nhỏ nhất).
Ý tưởng thuật toán Prim
Thuật toán Prim sẽ bắt đầu bằng việc chọn ngẫu nhiên một đỉnh bất kì và tiếp tục thêm các cạnh có trọng số nhỏ nhất cho đến khi có đủ tập hợp các đỉnh. Các bước để thực hiện:
- Bước 1. Khởi tạo tập hợp đỉnh V rỗng, tập hợp cạnh E rỗng.
- Bước 2. Chọn ngẫu nhiên 1 đỉnh và thêm vào tập hợp các đỉnh V.
- Bước 3. Chọn 1 đỉnh chưa có trong tập V mà có kết nối với 1 đỉnh trong V, cạnh tạo từ 2 đỉnh đó phải là cạnh có trọng số nhỏ nhất và thêm vào tập hợp các cạnh E.
- Bước 4. Lặp lại bước 3 cho đến khi cây khung hoàn thành (Cách nhận biết cây khung hoàn thành là tất cả các đỉnh của cây khung đều đã xuất hiện trong V), cây khung nhỏ nhất là cây khung được tạo từ tập các cạnh trong E.
Ví dụ của thuật toán Prim
Nếu bạn cảm thấy chưa hiểu rõ thì đừng lo chúng ta sẽ đi vào phần ví dụ và hình ảnh chắc chắn bạn sẽ cảm thấy dễ hiểu hơn đấy.
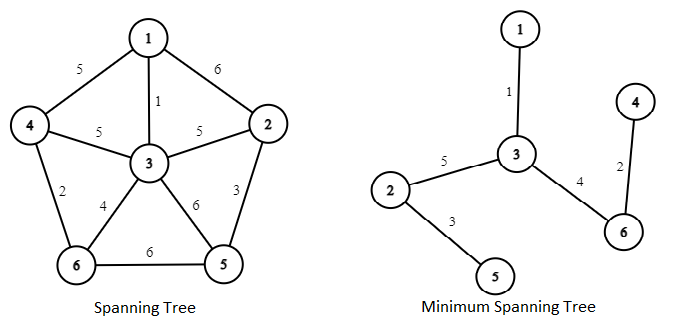
Hãy quan sát ví dụ với cây khung đầy đủ dưới đây.
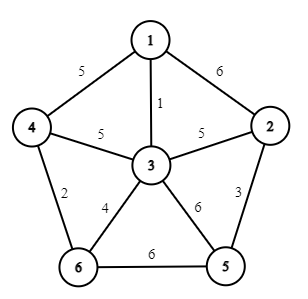
- Có đồ thị G=(V, E) Có V đỉnh và E cạnh.
- Tập hợp các đỉnh của đồ thị V = {1, 2, 3, 4, 5, 6} (Viết tắt của vertex nghĩa là đỉnh).
- Tập hợp các cạnh của E = {(1, 2), (1, 3), (1, 4), (2, 3), (2, 5), (3, 4), (3, 5), (3, 6), (4, 6), (5, 6)} (Viết tắt của edge nghĩa là cạnh).
- Ta tạo ra 2 tập hợp U và T, U là tập hợp các đỉnh và T là tập hợp các cạnh tạo ra cây khung nhỏ nhất.
- Ban đầu U={Ø} (rỗng) và T={Ø}.
Bước 1. Khởi tạo
- Ta tạo ra 2 tập hợp U và T, U là tập hợp các đỉnh và T là tập hợp các cạnh tạo ra cây khung nhỏ nhất.
- Ban đầu U={Ø} (rỗng) và T={Ø}.
Bước 2. Chọn 1 đỉnh ngẫu nhiên từ cây khung trên, ví dụ chúng ta chọn đỉnh 1. Sau bước này, ta có U={1} và T={Ø}.
![]()
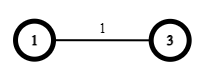
Bước 3. Tìm tất cả các cạnh có 1 đỉnh ở trong U. Ở đây, ta sẽ tìm được cạnh (1, 3) do khoảng cách nhỏ nhất với giá trị là 1. Sau bước này ta có U={1, 3} và T={(1, 3)}.
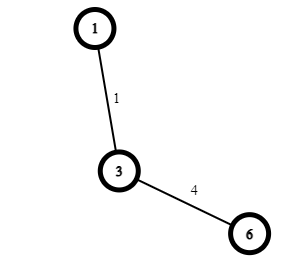
Bước 4. Tương tự bước 3, ta đi tìm cạnh nhỏ nhất có 1 đỉnh trong U mà cạnh đó chưa có trong V. Kết quả là ta tìm ra cạnh (3, 6) với giá trị 4. Sau bước này ta có U={1, 3, 6} và T={(1, 3), (3, 6)}.
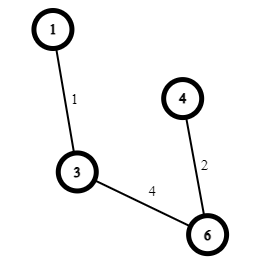
Bước 5. Do tập U mới chỉ có 3/6 đỉnh, ta tiếp tục đi tìm cạnh nhỏ nhất chưa khám phá mà 1 đỉnh của nó trong U. Kết quả là ta tìm được cạnh (6, 4). Bây giờ U={1, 3, 6, 4} và T={(1, 3), (3, 6), (6, 4)}.
Bước 6. Do tập U mới chỉ có 4/6 đỉnh, tiếp tục tìm cạnh nhỏ nhất chưa có trong T mà 1 đỉnh của nó trong U. Ta tìm được cạnh (3,2) với giá trị 5. Sau buớc này U={1, 3, 6, 4, 2} và T={(1, 3), (3, 6), (6, 4), (3, 2)}.
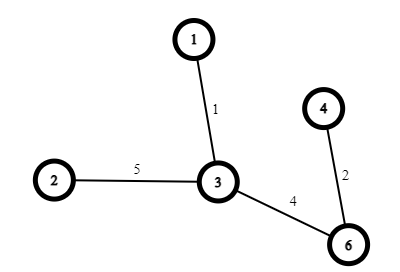
Bước 7. Do tập U mới chỉ có 5/6 đỉnh, tiếp tục tìm cạnh nhỏ nhất chưa có trong T mà 1 đỉnh của nó trong U. Ta tìm được cạnh (2, 5) với giá trị 3. Lúc này tập U đã có 6/6 đỉnh nên thuật toán kết thúc.
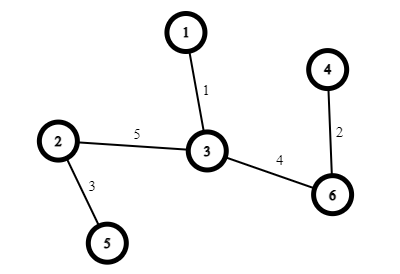
Hình ảnh động dưới đây mô phỏng lại quá trình tìm kiếm cây khung nhỏ nhất cho ví dụ từng bước ở trên:

Sau khi áp dụng xong thuật toán Prim, ta có U={1, 3, 6, 4, 2, 5} và T={(1, 3), (3, 6), (6, 4), (3, 2), (2, 5)}.
- Tập hợp các cạnh T={(1, 3), (3, 6), (6, 4), (3, 2), (2, 5)} tạo thành cây khung có tổng trọng số nhỏ nhất. Tổng trọng số của cây khung nhỏ nhất là:1 + 4 + 2 + 5 + 3 = 15
Code giải thuật Prim
Dưới đây là hàm chính thực thi giải thuật Prim biểu diễn đồ thi bằng ma trận kề, đi kèm với hướng dẫn bằng comment.
int prims(){
int cost[MAX][MAX];
int u,v,min_distance,distance[MAX],from[MAX];
int visited[MAX],no_of_edges,i,min_cost,j;
//Tạo cost[][](giá trị) của ma trận
for(i=0;i<n;i++)
for(j=0;j<n;j++)
{
if(G[i][j]==0)
//Nếu trong cây khung không có cạnh nối giữa 2 điểm i, j(Là G[i][j]==0)
cost[i][j]=infinity;
//Thì gán giá trị của cạnh i, j =infinity(Là 1 số cực lớn ở đây là 9999)
else
cost[i][j]=G[i][j];
//Nếu có cạnh nối giữa 2 điểm i, j thì gán giá trị của cạnh =G[i][j]
spanning[i][j]=0;
}
//Khởi tạo visited[],distance[] and from[]
distance[0]=0;
visited[0]=1;
for(i=1;i<n;i++)
{
distance[i]=cost[0][i];
from[i]=0;
visited[i]=0;
}
min_cost=0; //Giá trị của cây khung
no_of_edges=n-1; //Số cạnh được thêm vào.
while(no_of_edges>0)
{
//Tìm đỉnh có khoảng cách nhỏ nhất đến cây
min_distance=infinity;
//Gán min_distance=infinity
for(i=1;i<n;i++)
if(visited[i]==0&&distance[i]<min_distance)
//Mục đích của việc gán min_distance=infinity là để xác nhận distance[i] khác 0
{
v=i;
min_distance=distance[i];
}
u=from[v];
//Chèn cạnh vào cây khung
spanning[u][v]=distance[v];
spanning[v][u]=distance[v];
no_of_edges--;
visited[v]=1;
//Cập nhật distance[](khoảng cách) vào mảng
for(i=1;i<n;i++)
if(visited[i]==0&&cost[i][v]<distance[i])
{
distance[i]=cost[i][v];
from[i]=v;
}
min_cost=min_cost+cost[u][v];
}
return(min_cost);
}
Full code thuật toán Prim
#include<stdio.h>
#define infinity 9999
#define MAX 20
int G[MAX][MAX],spanning[MAX][MAX],n;
int prims();
int ReadMatrix(char filepath[] );
void OutputMatrix();
int ReadMatrix(char filepath[] )
{
FILE* f = fopen(filepath,"r");
if(f==NULL)
{
printf("nCant open file");
return 0;
}
fscanf(f,"%d", &n);
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
fscanf(f,"%d", &G[i][j]);
fclose(f);
return 1;
}
void OutputMatrix()
{
printf("Number of Vertices: %dn", n);
for(int i=0;i<n;i++)
{
printf("n");
for(int j=0;j<n;j++)
printf("%dt",G[i][j]);
}
}
int main()
{
int i,j,total_cost;
ReadMatrix("Prim.txt");
total_cost=prims();
printf("nSpanning Tree Matrix:n");
OutputMatrix();
printf("nnTotal cost of spanning tree=%d",total_cost);
return 0;
}
int prims()
{
int cost[MAX][MAX];
int u,v,min_distance,distance[MAX],from[MAX];
int visited[MAX],no_of_edges,i,min_cost,j;
for(i=0;i<n;i++)
for(j=0;j<n;j++)
{
if(G[i][j]==0)
cost[i][j]=infinity;
else
cost[i][j]=G[i][j];
spanning[i][j]=0;
}
distance[0]=0;
visited[0]=1;
for(i=1;i<n;i++)
{
distance[i]=cost[0][i];
from[i]=0;
visited[i]=0;
}
min_cost=0; //cost of spanning tree
no_of_edges=n-1; //no. of edges to be added
while(no_of_edges>0)
{
min_distance=infinity;
for(i=1;i<n;i++)
if(visited[i]==0&&distance[i]<min_distance)
{
v=i;
min_distance=distance[i];
}
u=from[v];
spanning[u][v]=distance[v];
spanning[v][u]=distance[v];
no_of_edges--;
visited[v]=1;
for(i=1;i<n;i++)
if(visited[i]==0&&cost[i][v]<distance[i])
{
distance[i]=cost[i][v];
from[i]=v;
}
min_cost=min_cost+cost[u][v];
}
return(min_cost);
}Dữ liệu vào:
6
0 6 1 5 0 0
6 0 5 0 3 0
1 5 0 5 6 4
5 0 5 0 0 2
0 3 6 0 0 6
0 0 4 2 6 0
Lưu ý:
- Một số giáo trình hay một vài nơi sẽ ghi số 0 thành kí hiệu vô cùng.
- Khi tạo file .txt thì nên bỏ chung cùng thư mục với bài làm để tránh sai sót không đáng có.
Kết quả thực thi của code theo ví dụ đầu vào phía trên:
Spanning Tree Matrix: Number of Vertices: 6 0 6 1 5 0 0 6 0 5 0 3 0 1 5 0 5 6 4 5 0 5 0 0 2 0 3 6 0 0 6 0 0 4 2 6 0 Total cost of spanning tree=15
Độ phức tạp thuật toán
| Cấu trúc dữ liệu tìm cạnh có trọng số nhỏ nhất | Độ phức tạp |
| Tìm kiếm trên ma trận kề | O(V2) |
| Đống nhị phân và danh sách kề | O((V + E) log V) = O(E log V) |
| Đống Fibonacci và danh sách kề | O(E + V log V) |
Code cài đặt phía trên đang sử dụng tìm kiếm trên ma trận kề có độ phức tạp là O(V2). Bạn cũng có thể cài đặt lại thuật toán Prim sử dụng danh sách kề.
Ứng dụng của cây khung nhỏ nhất
Với bài toán tìm cây khung nhỏ nhất, chúng ta có thể áp dụng để giải quyết & tối ưu rất nhiều bài toán trong thực tế. Ví dụ với bài toán lắp đặt hệ thống mạng cho 1 trường học:
- Tất cả các phòng cần có kết nối internet.
- Biết trước khoảng cách giữa 2 phòng bất kỳ
- Bài toán: Làm sao lắp đặt hệ thống mạng cho trường học này với chi phí tối thiếu (giả sử chi phí tỉ lệ thuận với khoảng cách).
Trên đây là nội dung bài viết về thuật toán Prim đi kèm code sử dụng ngôn ngữ C. Trong quá trình viết khó tránh khỏi sai sót , nếu có thắc mắc hay góp ý thì hãy bình luận bên dưới hoặc qua nhóm Lập Trình Không Khó để giải đáp thêm các thắc mắc các bạn vướng phải trong quá trình tìm hiểu.


Để lại một bình luận