Giải bài toán xếp hậu bằng đệ quy dùng code C/C++

Bài toán xếp xếp hậu là bài toán đặt tám quân hậu trên bàn cờ vua kích thước 8×8 sao cho không có quân hậu nào có thể “ăn” được quân hậu khác, hay nói khác đi không quân hậu nào có để di chuyển theo quy tắc cờ vua.

Giới thiệu bài toán xếp hậu

Lời giải của bài toán là một cách xếp tám quân hậu trên bàn cờ sao cho không có hai quân nào đứng trên cùng hàng, hoặc cùng cột hoặc cùng đường chéo. Bài toán tám quân hậu có thể tổng quát hóa thành bài toán đặt n quân hậu trên bàn cờ n×n(n ≥ 4).

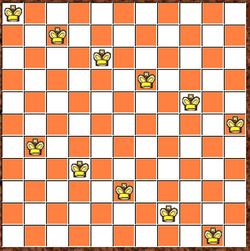
Hình ảnh ở trên mô tả một lời giải của bài toán xếp 11 quân hậu trên một bàn cờ vua 11*11. Vậy chúng ta cùng bắt tay vào tìm lời giải cho bài toán này.

Giải bài toán xếp hậu bằng đệ quy trong C/C++

• Để tiện trình bày ta dùng biến i để đánh dấu các hàng từ trên xuống ( 1 đến n). Dùng biến j để đánh dấu các cột từ trái sang phải ( 1 đến n );
• Các phần tử nằm trên cùng hàng có chỉ số hàng bằng nhau;
• Các phần tử nằm trên cùng cột có chỉ số cột bằng nhau;
• Để tiện cho việc in kết quả ra thì ta chỉ in ra chỉ số các cột tuần tự theo các hàng từ trên xuống.
• Điều kiện để đặt một quân hậu đúng chỗ là không có 2 trên cùng một cột ( chỉ số cột khác nhau). Không có 2 quân hậu nào cùng ở trên một đường chéo.

Ý tưởng:

• Đầu tiên ta đặt quân hậu thứ nhất vào các cột trên hàng 1 ( có n cách đặt ).
• Thử đặt quân hậu 2 vào từng cột ở hàng 2 sao cho không bị quân hậu 1 khống chế. Với mỗi vị trí của quân hậu này ta lại thử đặt quân hậu thứ ba vào các cột sao cho không bị các quân hậu trước khống chế.
• Sau khi đặt xong quân hậu thứ tám thì in ra một cách đặt.

Code C

#include<stdio.h>
#include<math.h>
int a[20];
bool Ok(int x2,int y2){
	//kiểm tra cách đặt có thỏa mãn không
	for(int i = 1; i < x2 ;i++)
		if(a[i] == y2 || abs(i-x2) == abs(a[i] - y2) )
			return false;
	//Nếu kiểm tra hết các trường hợp vẫn không sai thì trả về true
	return true;
}

void Xuat(int n){
	//in ra một kết quả
	for(int i=1;i<=n;i++)
		printf(" %d",a[i]);
	printf("n");
}

void Try(int i,int n){
	for(int j = 1;j<=n;j++){
		// thử đặt quân hậu vào các cột từ 1 đến n
		if(Ok(i,j)){
			//nếu cách đặt này thỏa mãn thì lưu lại vị trí
			a[i] = j;
                        //nếu đặt xong quân hậu thứ n thì xuất ra một kết quả
			if(i==n) Xuat(n);
			Try(i+1,n);
		}
	}
}

int main(){
	int n = 8;// ở đây mình cho bài toán là 8 quân hậu trên bàn 8*8
	Try(1,n);
	return 0;
}

Sau khi chạy thì sẽ ra các kết quả ( mình chỉ copy một ít kết quả thôi )

 1 5 8 6 3 7 2 4
 1 6 8 3 7 4 2 5
 1 7 4 6 8 2 5 3
 1 7 5 8 2 4 6 3

Mình giải thích một ít câu lệnh trong chương trình trên

• ( x2, y2) là vị trí mà quân hậu sẽ đặt vào. Như vậy chúng ta chúng ta đã đặt xong x2-1 quân hậu rồi.
• Để kiểm tra quân hậu này có bị các quân hậu trước khống chế hay không. Ta sẽ kiểm tra lần lượt các quân hậu ở trước với quân hậu vừa mới đặt vào.
• Chỉ cần bị một quân hậu khác khống chế thì vị trí này không thể đặt vào ( return false).
• a[i] == y2 dùng để kiểm tra xem quân hậu này có nằm cùng một cột với các quân hậu trước đó.
• abs(i - x2) == abs( a[i] - y2 ) dùng để kiểm tra xem quân hậu này có nằm trên đường chéo của các quân hậu trước đó hay không. Các bạn có thể vẽ hình ra và tự chứng minh nhé !

Bài viết mình đến đây là kết thúc. Cám ơn các bạn đã theo dõi !