Lập Trình Không Khó

Học lập trình theo cách riêng của bạn!

Bạn đang ở:Trang chủ / CTDL và Giải thuật / Cấu trúc dữ liệu / Cây Đỏ Đen (Red-Black Tree) – Phần 2 (Insert)

Cây Đỏ Đen (Red-Black Tree) – Phần 2 (Insert)

by Để lại bình luận

Ở bài trước, chúng ta đã tìm hiểu sơ qua về cây đỏ đen – Red Black Tree. Còn trong bài viết này, ta sẽ cùng nhau đi tìm hiểu cách để thêm (insert) một node vào cây đỏ đen.

Phần 1: Cây Đỏ Đen (Red-Black Tree) – Phần 1 (Giới thiệu)

1. Ôn lại kiến thức và Quy ước gọi tên

red black tree

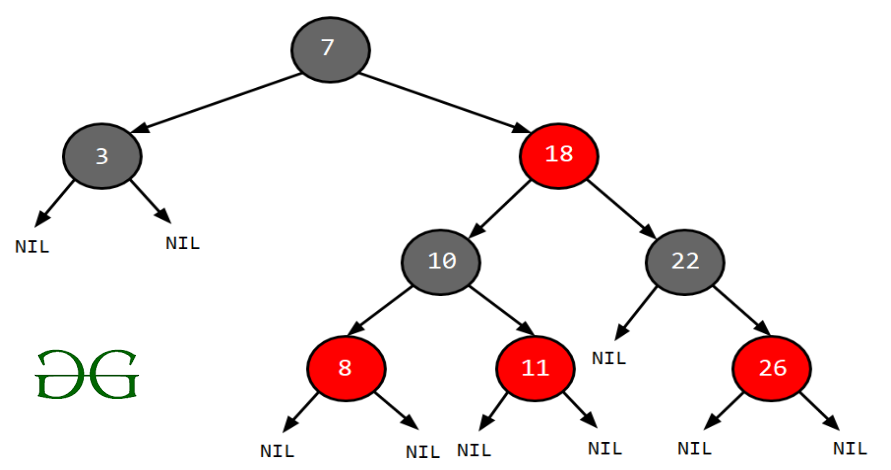
Trước khi bắt đầu thì chúng ta nên ôn lại kiến thức một tý: cây đỏ đen là gì? Nó như thế nào? Có những quy tắc chi? Cây đỏ đen là cây mà mọi node đều có thêm thuộc tính bit – quy định màu sắc (đỏ hoặc đen). Trong đó có 2 trong 5 quy tắc rất quan trọng:

        1. Không có hai node đỏ liền kề (Một node đỏ thì không thể có cha đỏ hoặc con đỏ).
        2. Mọi đường dẫn từ một node đến bất kì node NULL (thuộc con của nó ) thì đều có cùng số lượng node đen.

Về cách gọi tên các Node:

name

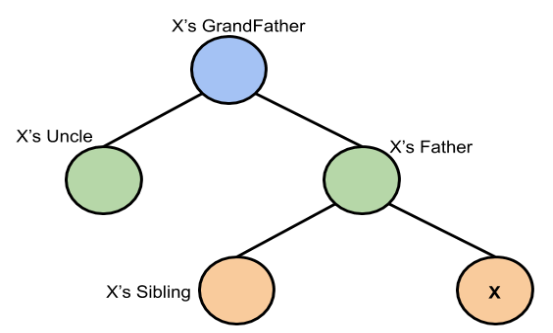
x->parent: đây được gọi là Node cha của x.

x->parent->left: đây là Node anh em của x (có thể right, tùy trường hợp)

x->parent->parent: chính là Node ông của x

x->parent->parent->left: được gọi là Node chú của x (có thể right, tùy trường hợp)

Note: Root (R viết hoa) là từ dùng để chỉ root của cả cây đỏ đen. Còn root thì dùng để chỉ node đang nằm trong các hàm.

2. Cấu trúc dữ liệu và cách để insert

a) Nhắc lại cây AVL

Đối với cây AVL mình chỉ cần tạo một struct Node rồi sau đó sử dụng đệ quy để thêm vào cây. Bởi vì tất cả các node của cây AVL đều có vai trò như nhau, bình đẳng nhau (kể cả root) nên mới sử dụng đệ quy như vậy được.

struct Node {
    int data;
    Node* left;
    Node* right;
    int height;
};
Node* Insert(Node* root, int value) {
    // Tìm kiếm vị trí rồi thêm vào
    if (root == NULL)
        return new Node{ value, NULL, NULL, 1 }; // Trả về Node có height = 1
    if (value > root->data)
        root->right = Insert(root->right, value);
    else if (value < root->data)
        root->left = Insert(root->left, value);
    else
        return root; // Neu bang thi khong them
    // Xử lí ...

b) Về Red-Black Tree

Đối với cây đỏ đen, ta không cần biết chiều cao của cây bằng bao nhiêu như cây AVL. Thay vào đó ta cần phải biết node cha (parent) màu gì? Có cùng màu đỏ với con hay không? Vậy nên phải thêm vào một con trỏ nữa, và tất nhiên là không thể thiếu thuộc tính color – chỉ màu sắc của một node với:

            • 1 – True : Chỉ màu đỏ
            • 0 – False: Chỉ màu đen
struct Node {
	int data;
	Node* left;
	Node* right;
	Node* parent;
	bool color;
	//1 -> Red   | 0 -> Black
};

Tuy nhiên, khác với cây AVL, các node của RBTree không bình đẳng. Có một node đặc biệt, đó chính là Root. Node Root luôn luôn phải mang màu đen – quy tắc 2. Do đó mình sẽ tạo thêm một struct RBTreenhằm kiểm soát được Root.

Các bạn đọc sơ qua code, rồi xem kĩ lại theo thứ tự phía dưới nha:

struct RedBlackTree {
    Node* Root;
    RedBlackTree() {
        Root = NULL;
    }
    Node* insertHelp(Node* root, int key) {
        if (root == NULL) {
            // Luôn luôn thêm node đỏ
            return new Node{ key, NULL, NULL, NULL, 1 }; // RED Node
        }
        else if (root != NULL && key < root->data) {
            // Node X : root->left
            // X->parent : root 
            root->left = insertHelp(root->left, key);
            root->left->parent = root;
        }
        else {
            // Node X    : root->right
            // X->parent : root
            root->right = insertHelp(root->right, key);
            root->right->parent = root;
        }
        return root;
    }

    void Insert(int key) {
        if (Root == NULL) {
                // Root luôn màu đen
            Root = new Node{ key, NULL, NULL, NULL, 0 };
        }
        else {
            Root = insertHelp(Root, key);
            if (Root->color == 1)
                Root->color = 0;
        }
}
  1. Node* Root: mình phải luôn luôn kiểm soát được màu sắc Node này.
  2. RedBlackTree(): đây là Constructor – hàm khởi tạo (xem thêm tại Lập trình hướng đối tượng). Hiểu đơn giản là khi mình khởi tạo 1 đối tượng RedBlackTree tree. Thì khi đó mặc định tree->Root = NULL.
  3. Insert(): Hàm này dùng để thêm 1 node vào nhưng… nó chỉ quan tâm đến node Root. Nếu Root == NULL thì gán vào Root với màu đen. Ngược lại nếu Root != NULL thì chỉ cần giao cho một hàm khác giải quyết – insertHelp(). Giả sử hàm này vô tình đổi màu Root thành màu đỏ thì chỉ cần tô lại đen.
  4. insertHelp(): Khi Root đã được xử lí riêng thì tất cả các node còn lại đều bình đẳng. Do đó ta chỉ cần sử dụng đệ quy như cây AVL để thêm node mới vào. Tuy nhiên, vì có thêm thuộc tính parent nên sau thêm ta phải gán giá trị của parent vào.

Lưu ý: Các node mới được thêm vào luôn luôn màu đỏ.

Tại sao ư? Ở bài trước, mình có nói: không thể có 3 node đen liên tiếp. Giả sử bạn thêm một node đen vào thì phải kiểm tra node cha có màu đen hay không? Node ông có màu đen không? Chưa kể, bạn phải kiểm tra các đường đi có số node đen bằng nhau không? Quá phức tạp.

Tuy nhiên nếu mình thêm node đỏ thì sao? Các đường đi vẫn đảm bảo số node đen bằng nhau vì mình chả thêm node đen nào cả. Và mình chỉ cần kiểm tra node cha, nếu màu đen thì ok – ổn, còn nếu màu đỏ thì chỉ cần xử lí xung đột đỏ.

3. Các phép quay cây đỏ đen

Hoàn toàn tương tự như cách quay cây AVL, RBTree cũng có hai cách quay đó là: quay phải, quay trái. Khác một tý là các bạn phải gán lại parent cho những node bị thay đổi. Và ngoài ra, lúc quay không đụng gì đến màu sắc nên bạn không cần phải để ý đâu.

a) Kỹ thuật quay phải – rotateRight

turn right

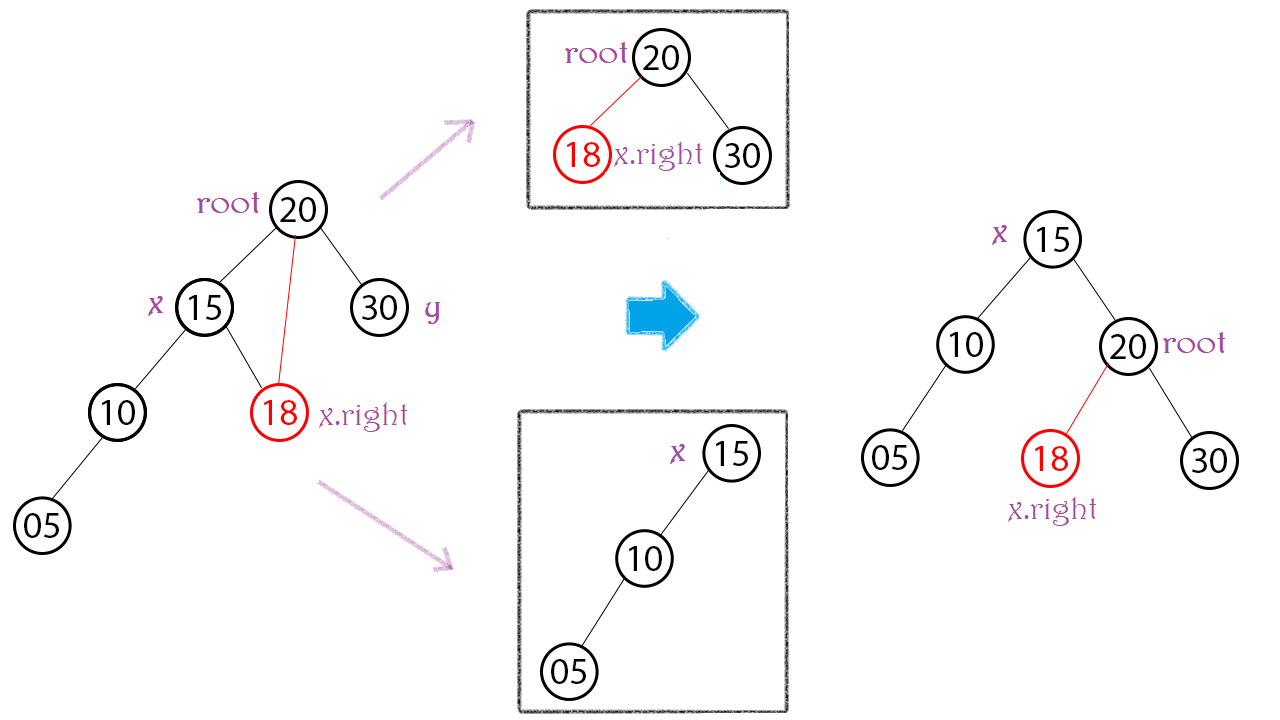
Gọi Node x, y lần lượt là các con trái, phải của root. Bây giờ, ta chỉ cần chú ý đến 3 Node: root, x, x.right.

Con trái của root không còn là x nữa mà là x.right hay  root.left = x.right

Nếu x.right != NULL thì x.right->parent = root

X sẽ lên làm Node cha với con phải là root hay x.right = root

Khi đó cha của root là x ==> root.parent = x

Trả về x

Node* rotateRight(Node* root) {
	Node* x = root->left;
	// Gán x->right vào left root
	root->left = x->right;
	if (x->right != NULL)
		x->right->parent = root;

	// Gán root vào x.right
	x->right = root;
	root->parent = x;

	// Trả về x
	return x;
}

b) Kỹ thuật quay trái – rotateLeft

turn left

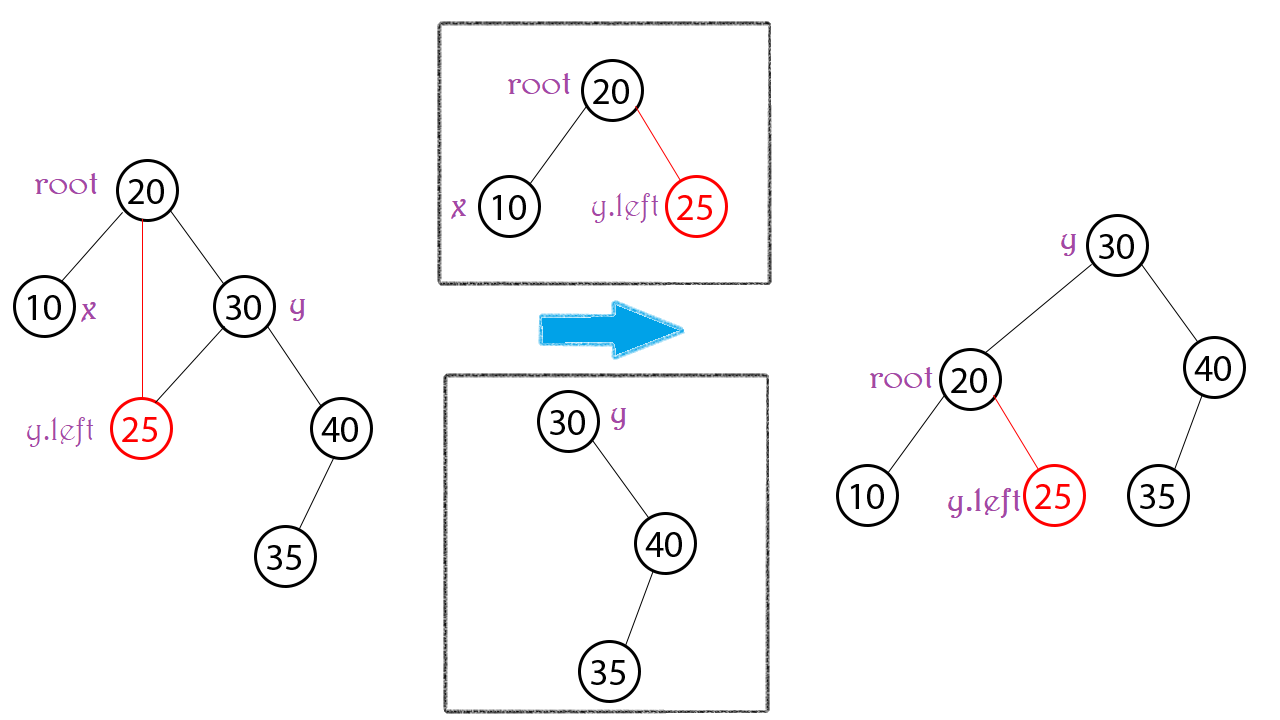
Hoàn toàn tương tự, gọi x y lần lượt là các con trái phải của root. Và ta chỉ cần quan tâm 3 Node: root, y, y.left

Node* rotateLeft(Node* root) {
	Node* y = root->right;
	// Gán y->left vào right root
	root->right = y->left;
	if (y->left != NULL)
		y->left->parent = root;

	// Gán root vào y.left
	y->left = root;
	root->parent = y;

	// Trả về y;
	return y;
}

4. Xử lí xung đột đỏ – insertHelp()

Khi ta thêm một node đỏ X vào cây, sẽ có 3 trường hợp xảy ra:

    1. Node cha màu đen. (Hoàn toàn ok – không cần xử lí gì cả)
    2. Node cha màu đỏ, Node chú cũng màu đỏ.
    3. Node cha màu đỏ, Node chú màu đen

Note: Node cha đỏ thì Node ông chắc chắn màu đen

1. Cha đỏ – Chú đỏ

parent uncle red

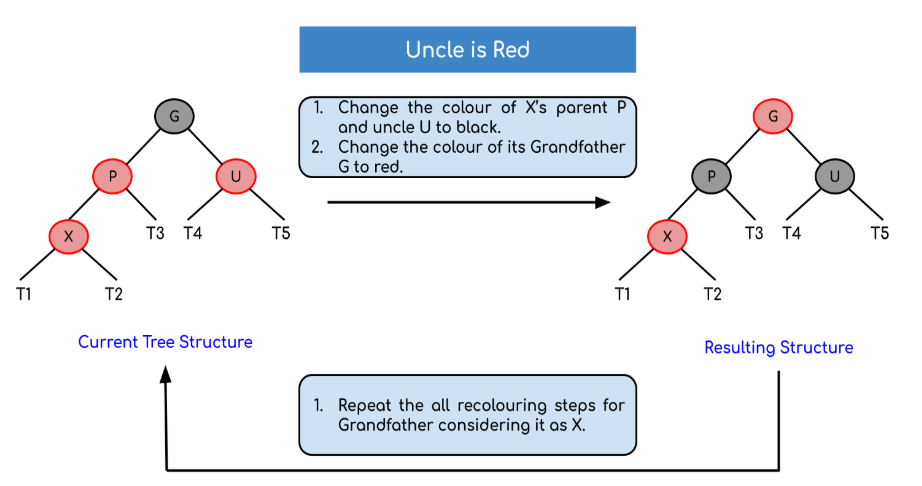
Cách xử rất đơn giản, chỉ cần đổi màu 3 node sau:

    • Node cha: đỏ => đen
    • Node chú: đỏ => đen
    • Node ông: đen => đỏ
// root chính là X->parent nha
if (root->parent->right == root){
    // Nếu X->parent là con phải của Node ông 
    root->color = root->parent->left->color = 0;
    if (root != Root)
        root->parent->color = 1;
}
else{
    // Nếu X->parent là con trái của Node ông 
    root->color = root->parent->right->color = 0;
    if (root != Root)
        root->parent->color = 1;
}

Về cơ bản thì cây con trên đã cân bằng và thỏa mãn 5 qui tắc cây đỏ đen. Tuy nhiên sẽ có người hỏi rằng: Node ông màu đỏ, nếu cha của node ông cũng màu đỏ thì sao? Thì mình sẽ xử lí tiếp thôi, ở đây mình sử dụng đệ quy nên nó sẽ dần dần truy hồi đến các Node tổ tiên. Gặp xung đột đỏ ở đâu thì xử lí ở đó.

2. Cha đỏ – Chú đỏ

Sẽ có 4 trường hợp: Trái trái, Trái phải, Phải phải, Phải phải, Phải trái. Cách xử lí thì hoàn toàn tương tự cây AVLchỉ thêm bước tô màu.

a) Trái trái – Left left case

leftleft

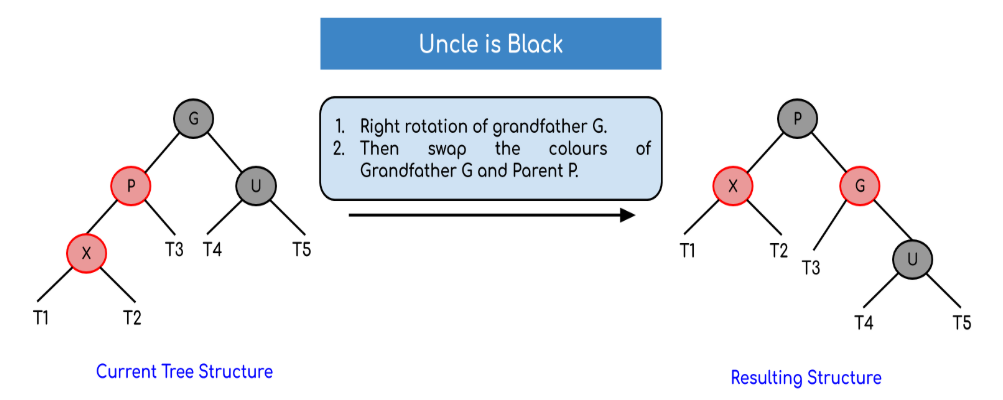
Xảy ra khi:

Node cha: là con trái của ông

Node X   : là con trái của cha

Xử lí:

      1. Quay phải Node ông
      2. Node cha: đỏ -> đen
      3. Node ông: đen -> đỏ

b) Trái phải – Left right case

leftright

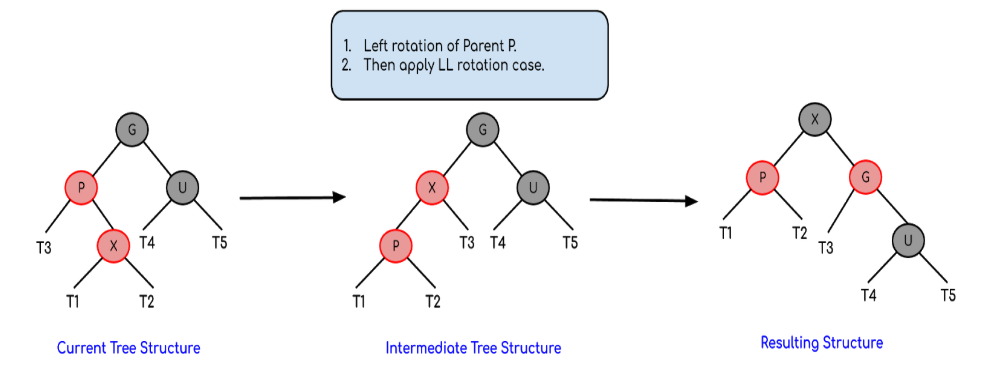
Xảy ra khi:

Node cha: là con trái của ông

Node X   : là con phải của cha

Xử lí:

      1. Quay trái Node cha (Đưa về Left left case)
      2. Xử lí y như trường hợp Trái trái

c) Phải phải – Right right case

rightright

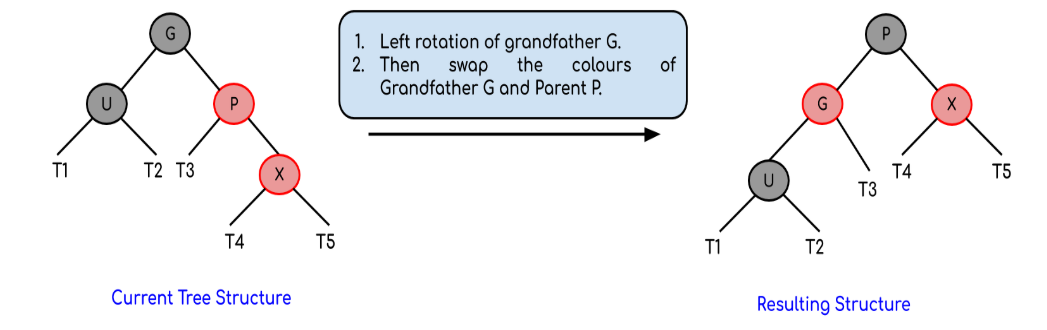
Xảy ra khi:

Node cha: là con phải của ông

Node X   : là con phải của cha

Xử lí:

      1. Quay trái Node ông
      2. Node cha: đỏ -> đen
      3. Node ông: đen -> đỏ

d) Phải trái – Right right case

rightleft

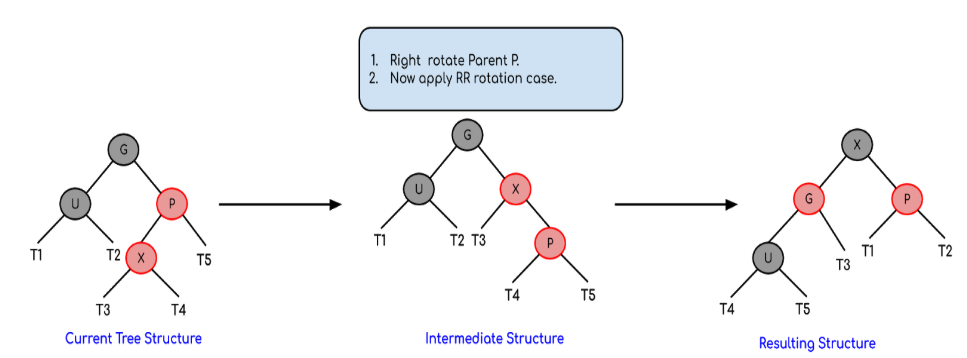
Xảy ra khi:

Node cha: là con phải của ông

Node X   : là con trái của cha

Xử lí:

      1. Quay phải Node cha (Đưa về Right right case)
      2. Xử lí y như trường hợp Phải phải

5. Code chính

#include <iostream>
#include <cmath>

using namespace std;
#define COUNT 10

struct Node {
	int data;
	Node* left;
	Node* right;
	Node* parent;
	bool color;
	//1 -> Red   | 0 -> Black
};

Node* rotateRight(Node* root) {
	Node* x = root->left;
	// Gán x->right vào left root
	root->left = x->right;
	if (x->right != NULL)
		x->right->parent = root;

	// Gán root vào x.right
	x->right = root;
	root->parent = x;

	// Trả về x
	return x;
}

Node* rotateLeft(Node* root) {
	Node* y = root->right;
	// Gán y->left vào right root
	root->right = y->left;
	if (y->left != NULL)
		y->left->parent = root;

	// Gán root vào y.left
	y->left = root;
	root->parent = y;

	// Trả về y;
	return y;
}

struct RedBlackTree {
	Node* Root;
	bool ll = false;
	bool rr = false;
	bool lr = false;
	bool rl = false;
	RedBlackTree() {
		Root = NULL;
	}
	Node* insertHelp(Node* root, int key) {
		// f đúng khi có xung đột RED RED
		bool f = false;

		if (root == NULL) {
			return new Node{ key, NULL, NULL, NULL, 1 }; // RED Node
		}
		else if (key < root->data) {
			root->left = insertHelp(root->left, key);
			root->left->parent = root;
			// root->left = Node X
			// root       = X->parent
			if (Root != root) {
				if (root->color == root->left->color == 1)
					f = true;
			}
		}
		else {
			root->right = insertHelp(root->right, key);
			root->right->parent = root;
			// root->right = Node X
			// root        = X->parent
			if (Root != root) {
				if (root->color == root->right->color == 1)
					f = true;
			}
		}

		// Xử lý 4 TH lệch
		// *** Khi này (ll, lr, rr, rl = false) nên chưa xử lí liền
		// *** Sau khi thoát 1 vòng đệ quy thì: root = X->parent->parent 
		// *** Tức là Node ông, lúc này ta quay Node ông 
		// Case 1 : Left left - Trái trái
		if (ll) {
			root = rotateRight(root);
			root->color = 0;
			root->right->color = 1;
			ll = false;
		}
		// Case 2 : Right right - Phải phải
		else if (rr) {
			root = rotateLeft(root);
			root->color = 0;
			root->left->color = 1;
			rr = false;
		}
		// Case 3 : Left right - Phải trái
		else if (lr) {
			root->left = rotateLeft(root->left);
			root->left->parent = root;

			root = rotateRight(root);
			root->color = 0;
			root->right->color = 1;
			lr = false;
		}
		// Case 4 : Right left - Phải trái
		else if (rl) {
			root->right = rotateRight(root->right);
			root->right->parent = root;

			root = rotateLeft(root);
			root->color = 0;
			root->left->color = 1;
			rl = false;
		}

		// Xử lí xung đột đỏ - RED RED
		if (f) {
			if (root->parent->right == root) {
				if (root->parent->left == NULL || root->parent->left->color == 0) {
					// Cha đỏ - chú đen (rr or rl)
					if (root->left != NULL && root->left->color == 1)
						rl = true;
					if (root->right != NULL && root->right->color == 1)
						rr = true;
				}
				else {
					// Cha đỏ - chú đỏ
					root->color = root->parent->left->color = 0;
					if (root != Root)
						root->parent->color = 1;
				}
			}
			else {
				if (root->parent->right == NULL || root->parent->right->color == 0) {
					// Cha đỏ - chú đen (ll or lr)
					if (root->left != NULL && root->left->color == 1)
						ll = true;
					if (root->right != NULL && root->right->color == 1)
						lr = true;
				}
				else {
					// Cha đỏ - chú đỏ
					root->color = root->parent->right->color = 0;
					if (root != Root)
						root->parent->color = 1;
				}
			}
			f = false;
		}
		return root;
	}

	void Insert(int key) {
		if (Root == NULL) {
			Root = new Node{ key, NULL, NULL, NULL, 0 };
		}
		else {
			Root = insertHelp(Root, key);
			if (Root->color == 1)
				Root->color = 0;
		}
	}
};

string getColor(Node* root) {
	if (root->color == 1)
		return "RED";
	return "BLACK";
}

// In - Print 2D ra console
void print2DUtil(Node* root, int space) {
	if (root == NULL)
		return;
	space += COUNT;

	print2DUtil(root->right, space);
	cout << endl;

	for (int i = COUNT; i < space; i++)
		cout << " ";
	cout << root->data << " (" << getColor(root) << ") " << "n";

	print2DUtil(root->left, space);
}

void print2D(Node* root) {
	print2DUtil(root, 0);
}


int main() {
	RedBlackTree RBTree;
	RBTree.Insert(1);
	RBTree.Insert(4);
	RBTree.Insert(6);
	RBTree.Insert(3);
	RBTree.Insert(5);
	RBTree.Insert(7);
	RBTree.Insert(8);
	RBTree.Insert(2);
	RBTree.Insert(9);

	print2D(RBTree.Root);
	return 0;
}

Kết quả:

                              9 (RED)

                    8 (BLACK)

                              7 (RED)

          6 (RED)

                    5 (BLACK)

4 (BLACK)

                    3 (RED)

          2 (BLACK)

                    1 (RED)

Cảm ơn các bạn đã đọc bài viết của mình. Nếu thấy hay thì hãy chia sẽ nó cho mọi người cùng đọc nhé!  Ngoài ra, bạn nào muốn tham khảo code các ngôn ngữ khác thì hãy truy cập vào Geeks for geeks – Red Black Tree – Set 2 | Insert.

Nguồn tham khảo: Geeks for Geeks

Bài tiếp theo, cũng là bài cuối của cây đỏ đen: Cây Đỏ Đen – Phần 3 (Delete)

4.5/5 - (2 bình chọn)

Bài viết liên quan

Danh sách liên kết đôi
Cài đặt danh sách liên kết đôi trong C/C++
Cài đặt danh sách liên kết đơn trong C
Danh sách liên kết đơn – Single linked list
Cây Đỏ Đen (Red-Black Tree) – Phần 3 (Delete)

Reader Interactions

Để lại một bình luận

Email của bạn sẽ không được hiển thị công khai. Các trường bắt buộc được đánh dấu *

DMCA.com Protection Status