Trong bài học này, bạn đọc sẽ cùng Lập Trình Không Khó tiếp tục luyện tập kiến thức về hàm đã được học trong khóa học Học C Bá Đạo ở các bài học trước. Lần này chúng ta sẽ giải quyết bài toán chuyển đổi số thập phân sang nhị phân và ngược lại, đổi số nhị phân sang hệ thập phân.
Cách đổi số thập phân sang nhị phân và ngược lại
[wpcc-iframe loading=”lazy” title=”Bài 37. Chuyển số nhị phân sang thập phân và ngược lại” width=”720″ height=”405″ src=”https://www.youtube.com/embed/CPKSENnEj2Y?list=PLh91SaQgRYnpj1GqVmVMq4acSAHtSKKwR” frameborder=”0″ allow=”accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share” allowfullscreen]
Đổi số thập phân sang nhị phân
Ví dụ hệ thập phân: 1234 = 1 * 10^3 + 2 * 10^2 + 3 * 10^1 + 4 * 10^0
Ví dụ hệ nhị phân: 101 = 1 * 2^2 + 0 * 2^1 + 1 * 2^0
Cách chuyển:
Ví dụ với n = 8, Ở mỗi bước ta thực hiện phép chia dư cho 2 để lấy số dư và sau đó thực hiện chia cho 2 cho tới khi n == 0.
0, 4 => 8 % 2 * 10 ^ 0
0, 2 => 4 % 2 * 10 ^ 1
0, 1 => 2 % 2 * 10 ^ 2
1, 0 => 1 % 2 * 10 ^ 3
=> Hệ nhị phân của 8 là 1000.

Dưới đây là lời giải tham khảo được viết bằng code C (code trong video phía trên).
/*
Chuyển số nhị phân sang thập phân.
Hệ thập phân: 1234 = 1 * 10^3 + 2 * 10^2 + 3 * 10^1 + 4 * 10^0
Hệ nhị phân: 101 = 1 * 2^2 + 0 * 2^1 + 1 * 2^0
Cách chuyển:
n = 8
0, 4 => 8 % 2 * 10 ^ 0
0, 2 => 4 % 2 * 10 ^ 1
0, 1 => 2 % 2 * 10 ^ 2
1, 0 => 1 % 2 * 10 ^ 3
int kq = 1000
*/
#include <stdio.h>
#include <math.h>
long long Dec2Bin(int decimalNumber) // Ctrl H => find & replace
{
long long binaryNumber = 0;
int p = 0;
while (decimalNumber > 0)
{
binaryNumber += (decimalNumber % 2) * pow(10, p);
++p;
decimalNumber /= 2;
}
return binaryNumber;
}
int main()
{
int decimalNumber;
printf("nNhap so thap phan: ");
scanf("%d", &decimalNumber);
printf("Bin = %d", Dec2Bin(decimalNumber));
}
Kết quả chạy:
PS G:c_courcesday_37> .Dec2Bin.exe Nhap so thap phan: 127 Bin = 1111111 PS G:c_courcesday_37> .Dec2Bin.exe Nhap so thap phan: 8 Bin = 1000
Đổi số nhị phân sang thập phân
Chuyển số nhị phân sang thập phân.
Hệ thập phân: 1234 = 1 * 10^3 + 2 * 10^2 + 3 * 10^1 + 4 * 10^0
Hệ nhị phân: 101 = 1 * 2^2 + 0 * 2^1 + 1 * 2^0
Vậy nếu ta có số 1110 ở hệ nhị phân => Ta có 0 + 2 + 4 + 8 = 14 ở hệ thập phân.
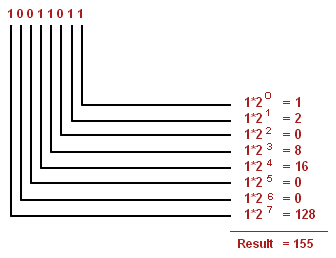
Dưới đây là lời giải tham khảo theo hướng dẫn từ trong video phía trên:
/*
Chuyển số nhị phân sang thập phân.
Hệ thập phân: 1234 = 1 * 10^3 + 2 * 10^2 + 3 * 10^1 + 4 * 10^0
Hệ nhị phân: 101 = 1 * 2^2 + 0 * 2^1 + 1 * 2^0
1110: 0 + 2 + 4 + 8 = 14
*/
#include <stdio.h>
#include <math.h>
int BinToDec(long long binaryNumber)
{
int p = 0;
int decNumber = 0;
while (binaryNumber > 0)
{
decNumber += (binaryNumber % 10) * pow(2, p);
++p;
binaryNumber /= 10;
}
return decNumber;
}
int main()
{
long long binaryNumber;
printf("nNhap so nhi phan: ");
scanf("%d", &binaryNumber);
printf("Dec = %d", BinToDec(binaryNumber));
}
Kết quả chạy chương trình:
PS G:c_courcesday_37> .Bin2Dec.exe Nhap so nhi phan: 1110 Dec = 14 PS G:c_courcesday_37> .Bin2Dec.exe Nhap so nhi phan: 1111111 Dec = 127
Theo dõi lập trình không khó tại:



Để lại một bình luận