Thuật toán sắp xếp merge sort là một trong những thuật toán có độ phức tạp ở mức trung bình và cùng sử dùng phương pháp chia để trị giống thuật toán sắp xếp nhanh quick sort. Thuật toán này không chỉ áp dụng trong sắp xếp mà còn ở nhiều bài toán khác. Hãy cùng tìm tôi tìm hiểu nhé.
Chào mừng các bạn quay trở lại với blog của Nguyễn Văn Hiếu. Đây là một bài viết trong series các thuật toán sắp xếp có minh họa code sử dụng ngôn ngữ lập trình C++.
Ở bài viết này Nguyễn Văn Hiếu xin giới thiệu tới các bạn thuật toán sắp xếp merge sort. Đây là một thuật toán rất sắp xếp rất hay và có độ phức tạp thấp hơn.
Lưu ý: Bài viết chỉ mô tả cho việc sắp xếp dãy số tăng dần. Việc sắp xếp dãy số giảm dần sẽ tương tự và bạn đọc tự tìm hiểu
Ý tưởng của thuật toán merge sort
Giống như Quick sort, Merge sort là một thuật toán chia để trị. Thuật toán này chia mảng cần sắp xếp thành 2 nửa. Tiếp tục lặp lại việc này ở các nửa mảng đã chia. Sau cùng gộp các nửa đó thành mảng đã sắp xếp. Hàm merge() được sử dụng để gộp hai nửa mảng. Hàm merge(arr, l, m, r) là tiến trình quan trọng nhất sẽ gộp hai nửa mảng thành 1 mảng sắp xếp, các nửa mảng là arr[l…m] và arr[m+1…r] sau khi gộp sẽ thành một mảng duy nhất đã sắp xếp.
Hãy xem ý tưởng triển khai code dưới đây để hiểu hơn
mergeSort(arr[], l, r)
If r > l
1. Tìm chỉ số nằm giữa mảng để chia mảng thành 2 nửa:
middle m = (l+r)/2
2. Gọi đệ quy hàm mergeSort cho nửa đầu tiên:
mergeSort(arr, l, m)
3. Gọi đệ quy hàm mergeSort cho nửa thứ hai:
mergeSort(arr, m+1, r)
4. Gộp 2 nửa mảng đã sắp xếp ở (2) và (3):
merge(arr, l, m, r)Hình ảnh dưới đây từ wikipedia sẽ hiển thị cho bạn toàn bộ sơ đồ tiến trình của thuật toán merge sort cho mảng {38, 27, 43, 3, 9, 82, 10}. Nếu nhìn kỹ hơn vào sơ đồ này, chúng ta có thể thấy mảng ban đầu được lặp lại hành động chia cho tới khi kích thước các mảng sau chia là 1. Khi kích thước các mảng con là 1, tiến trình gộp sẽ bắt đầu thực hiện gộp lại các mảng này cho tới khi hoàn thành và chỉ còn một mảng đã sắp xếp.
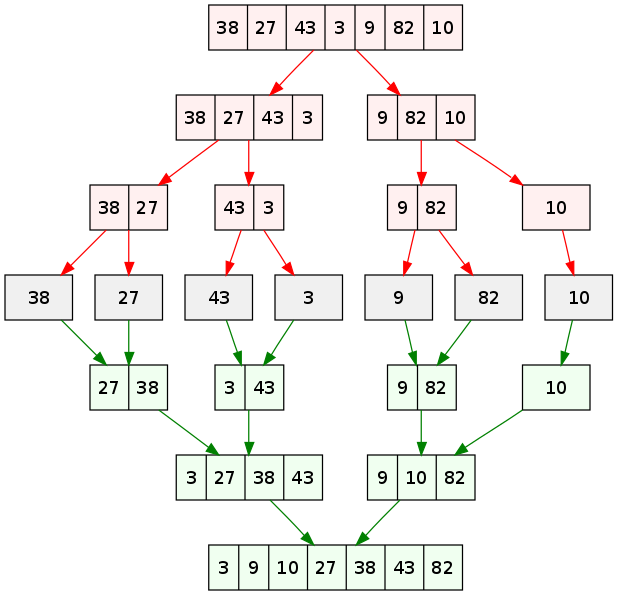
Cách hàm merge hoạt động khi gộp hai mảng con
Với trường hợp khi 2 mảng con chỉ có 1 phần tử, ta chỉ việc xem phần tử nào nhỏ hơn và đẩy lên đầu, phần tử còn lại đặt phía sau. Do vậy, các mảng con cần gộp lại có tính chất luôn được sắp tăng dần.
Giả sử ta có 2 mảng con lần lượt là: arr1 = [1 9 10 10] , n1 = 4 // chiều dài của mảng con arr2 = [3 5 7 9], n2 = 4 sort_arr = [] // Mảng lưu lại tiến trình gộp Khởi tạo i = 0, j = 0 tương ứng là chỉ số bắt đầu của arr1 và arr2 Xét thấy arr1[i] < arr2[j] => chèn arr1[i] vào cuối mảng sort_arr, tăng i lên 1 đơn vị => sort_arr = [1], i = 1 Xét thấy arr1[i] > arr2[j] => chèn arr2[j] vào cuối mảng sort_arr, tăng j lên 1 đơn vị => sort_arr = [1, 3], i = 1, j = 1 Xét thấy arr1[i] > arr2[j] => chèn arr2[j] vào cuối mảng sort_arr, tăng j lên 1 đơn vị => sort_arr = [1, 3, 5], i = 1, j = 2 Xét thấy arr1[i] > arr2[j] => chèn arr2[j] vào cuối mảng sort_arr, tăng j lên 1 đơn vị => sort_arr = [1, 3, 5, 7], i = 1, j = 3 Xét thấy arr1[i] = arr2[j] => chèn arr1[i] hoặc arr2[j] vào cuối mảng sort_arr Giả sử tôi chọn arr1, tăng i lên 1 đơn vị => sort_arr = [1, 3, 5, 7, 9], i = 2, j = 3 Xét thấy arr1[i] > arr2[j] => chèn arr2[j] vào cuối mảng sort_arr, tăng j lên 1 đơn vị => sort_arr = [1, 3, 5, 7, 9, 9], i = 1, j = 4 Do j >= n2, tiếp tục tăng i chừng nào i < n1 thi thêm phần tử ở arr1[i]ư vào sort_arr. Sau cùng ta được mảng đã sắp xếp là sort_arr = [1, 3, 5, 7, 9, 9, 10, 10]
Xem thêm: Chuyên mục cấu trúc dữ liệu và giải thuật
Minh họa thuật toán sắp xếp quick sort sử dụng C/C++
// Code from https://nguyenvanhieu.vn
#include<stdlib.h>
#include<stdio.h>
// Gộp hai mảng con arr[l...m] và arr[m+1..r]
void merge(int arr[], int l, int m, int r)
{
int i, j, k;
int n1 = m - l + 1;
int n2 = r - m;
/* Tạo các mảng tạm */
int L[n1], R[n2];
/* Copy dữ liệu sang các mảng tạm */
for (i = 0; i < n1; i++)
L[i] = arr[l + i];
for (j = 0; j < n2; j++)
R[j] = arr[m + 1+ j];
/* Gộp hai mảng tạm vừa rồi vào mảng arr*/
i = 0; // Khởi tạo chỉ số bắt đầu của mảng con đầu tiên
j = 0; // Khởi tạo chỉ số bắt đầu của mảng con thứ hai
k = l; // IKhởi tạo chỉ số bắt đầu của mảng lưu kết quả
while (i < n1 && j < n2)
{
if (L[i] <= R[j])
{
arr[k] = L[i];
i++;
}
else
{
arr[k] = R[j];
j++;
}
k++;
}
/* Copy các phần tử còn lại của mảng L vào arr nếu có */
while (i < n1)
{
arr[k] = L[i];
i++;
k++;
}
/* Copy các phần tử còn lại của mảng R vào arr nếu có */
while (j < n2)
{
arr[k] = R[j];
j++;
k++;
}
}
/* l là chỉ số trái và r là chỉ số phải của mảng cần được sắp xếp */
void mergeSort(int arr[], int l, int r)
{
if (l < r)
{
// Tương tự (l+r)/2, nhưng cách này tránh tràn số khi l và r lớn
int m = l+(r-l)/2;
// Gọi hàm đệ quy tiếp tục chia đôi từng nửa mảng
mergeSort(arr, l, m);
mergeSort(arr, m+1, r);
merge(arr, l, m, r);
}
}
/* Hàm xuất mảng */
void printArray(int A[], int size)
{
int i;
for (i=0; i < size; i++)
printf("%d ", A[i]);
printf("n");
}
int main()
{
int arr[] = {12, 11, 13, 5, 6, 7};
int arr_size = sizeof(arr)/sizeof(arr[0]);
printf("Given array is n");
printArray(arr, arr_size);
mergeSort(arr, 0, arr_size - 1);
printf("nSorted array is n");
printArray(arr, arr_size);
return 0;
}Đánh giá thuật toán sắp xếp merge sort
Độ phức tạp thuật toán
- Trường hợp tốt: O(nlog(n))
- Trung bình: O(nlog(n))
- Trường hợp xấu: O(nlog(n))
Không gian bộ nhớ sử dụng: O(n)


Để lại một bình luận