Thuật toán tìm ước chung lớn nhất trong C/C++

Trong bài viết này tôi sẽ cùng các bạn tìm hiểu về các thuật toán tìm ước chung lớn nhất của hai số nguyên và minh họa code bằng ngôn ngữ C/C++.

Định nghĩa ước chung lớn nhất

Ước chung lớn nhất (GCD – Greatest Common Divisor) của 2 số nguyên $a$ và $b$ là số nguyên lớn nhất $d$ thỏa mãn tính chất cả a và b đều chia hết cho d.

Các thuật toán tìm ước chung lớn nhất

Dưới đây là một số cách thường được sử dụng để giải quyết bài toán tìm ước chung lớn nhất của hai số.

Cách 1. Tìm UCLN sử dụng phép trừ

Đây là sơ đồ của thuật toán này

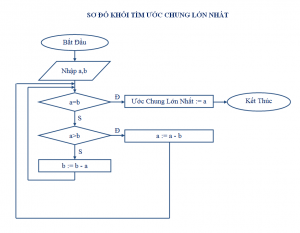
Code minh họa

// Code from https://nguyenvanhieu.vn

int gcd(int a, int b){
    // Nếu a = 0 => ucln(a,b) = b
    // Nếu b = 0 => ucln(a,b) = a
    if (a == 0 || b == 0){
        return a + b;
    }
    while (a != b){
        if (a > b){
            a -= b; // a = a - b
        }else{
            b -= a;
        }
    }
    return a; // return a or b, bởi vì lúc này a và b bằng nhau
}

Giải thích:

Tại mỗi bước lặp nó sẽ kiểm tra giá trị hiện tại của a và b xem thằng nào lớn hơn. 
Ví dụ với hai số a = 7, b = 5

L1: a > b => a = 2, b = 5
L2: b > a => a = 2, b = 3
L3: b > a => a = 2, b = 1
L4: a > b => a = 1, b = 1
L5: a == b => trả về a hoặc b đều được => KQ là 1

Xem thêm: Các chia sẻ hay được đúc kết từ kinh nghiệm của tác giả

Cách 2. Tìm UCLN sử dụng phép chia dư

Sơ đồ thuật toán tương tự như cách 1. Chỉ thay đổi phép trừ sang phép chia dư.

Code minh họa

// Code from https://nguyenvanhieu.vn

int gcd(int a, int b){
    // Lặp tới khi 1 trong 2 số bằng 0
    while (a*b != 0){ 
        if (a > b){
            a %= b; // a = a % b
        }else{
            b %= a;
        }
    }
    return a + b; // return a + b, bởi vì lúc này hoặc a hoặc b đã bằng 0.
}

Cách 3. Tìm UCLN sử dụng giải thuật Euclid

Cho a, b là hai số nguyên (giả sử a ≥ b), để tìm ước chung lớn nhất của hai số a và b ta cần thực hiện chia a cho b được thương q và số dư r (r ≥ 0) tức là a = b*q + r, khi đó ta có:

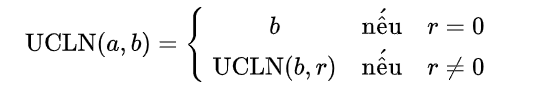
Cài đặt thuật toán sử dụng đệ quy.

// Code from https://nguyenvanhieu.vn

int gcd(int a, int b) {
    if (b == 0) return a;
    return gcd(b, a % b);
}

Cài đặt khử đệ quy

// Code from https://nguyenvanhieu.vn

int gcd(int a, int b) {
    int tmp;
    while(b != 0) {
        tmp = a % b;
        a = b;
        b = tmp;
    }
    return a;
}

Gợi ý: Một số bài viết về giải thuật tương tự

Cách 4. Tìm UCLN sử dụng hàm có sẵn của C++

Để có thể sử dùng hàm tìm ucln trong C++ ta cần thêm thư viện algorithm.

Ví dụ minh họa:

// Code from https://nguyenvanhieu.vn
#include <algorithm>
#include <stdio.h>
int main(){
    int a = 5, b = 9;
    printf("ngcd(%d, %d) = %d", a, b, std::__gcd(a,b));
}

Tổng kết tất cả cách cách trên trong 1 chương trình.

// Code from https://nguyenvanhieu.vn

#include <stdio.h>
#include <algorithm>
int gcd1(int a, int b){
    // Nếu a = 0 => ucln(a,b) = b
    // Nếu b = 0 => ucln(a,b) = a
    if (a == 0 || b == 0){
        return a + b;
    }
    while (a != b){
        if (a > b){
            a -= b; // a = a - b
        }else{
            b -= a;
        }
    }
    return a; // return a or b, bởi vì lúc này a và b bằng nhau
}

int gcd2(int a, int b){
    // Nếu a = 0 => ucln(a,b) = b
    // Nếu b = 0 => ucln(a,b) = a
    if (a == 0 || b == 0){
        return a + b;
    }
    // Lặp tới khi 1 trong 2 số bằng 0
    while (a*b != 0){
        if (a > b){
            a %= b; // a = a % b
        }else{
            b %= a;
        }
    }
    return a + b; // return a + b, bởi vì lúc này hoặc a hoặc b đã bằng 0.
}

int gcd3(int a, int b) {
    if (b == 0) return a;
    return gcd3(b, a % b);
}

int gcd4(int a, int b) {
    int tmp;
    while(b != 0) {
        tmp = a % b;
        a = b;
        b = tmp;
    }
    return a;
}

int main(){
    int a = 5, b = 9;
    printf("ngcd1(%d, %d) = %d", a, b, gcd1(a,b));
    printf("ngcd2(%d, %d) = %d", a, b, gcd2(a,b));
    printf("ngcd3(%d, %d) = %d", a, b, gcd3(a,b));
    printf("ngcd4(%d, %d) = %d", a, b, gcd4(a,b));
    printf("ngcd5(%d, %d) = %d", a, b, std::__gcd(a,b));
}

Kết quả chạy thử

gcd1(5, 9) = 1
gcd2(5, 9) = 1
gcd3(5, 9) = 1
gcd4(5, 9) = 1
gcd5(5, 9) = 1

Trên đây tôi đã trình bày chi tiết về các thuật toán tìm ước chung lớn nhất của hai số. Nếu bạn đọc quan tâm hay có thắc mắc gì. Vui lòng để lại ở bình luận phía cuối bài viết.

Nếu bạn quan tâm đến tìm BCNN của 2 số, vui lòng chuyển qua bài viết tìm BCNN của 2 số nhé.