Hướng dẫn cách tính lũy thừa ma trận – Ma trận là một chủ đề không còn xa lạ với những người dấn thân vào ngành lập trình. Trong hầu hết tất cả các nhánh của ngành IT như web, game, AI, lập trình thi đấu,… ma trận đều giữ một vị trí đặc biệt quan trọng. Hôm nay chúng ta sẽ tìm hiểu về phép lũy thừa ma trận, cách tối ưu cùng với tầm quan trọng của nó.
Nội dung bài viết gồm 3 phần, đầu tiên chúng ta sẽ đi tìm hiểu về phép nhân ma trận (bởi vì phép lũy thừa được thực hiện dựa trên phép nhân). Sau đó, chúng ta sẽ đi tìm hiểu về phép lũy thừa ma trận. Cuối cùng, chúng ta sẽ sử dụng ứng dụng của phép lũy thừa ma trận trong 1 bài toán rất điển hình là tính số fibonacci thứ N. Chúng ta cùng bắt đầu nhé.
Để có thể nắm rõ bài viết này, độc giả cần có kiến thức lập trình căn bản, bao gồm kiến thức cấu trúc điều khiển, vòng lặp, hàm đệ quy và mảng 2 chiều. Các kiến thức trên đều có trong khóa học C căn bản của LTKK.
Phép nhân ma trận
Trong toán học, ma trận (tiếng anh: Matrix) là một mảng chữ nhật– các số, ký hiệu, hoặc biểu thức, sắp xếp theo hàng và cột – mà mỗi ma trận tuân theo những quy tắc định trước. Từng ô trong ma trận được gọi là các phần tử hoặc mục.
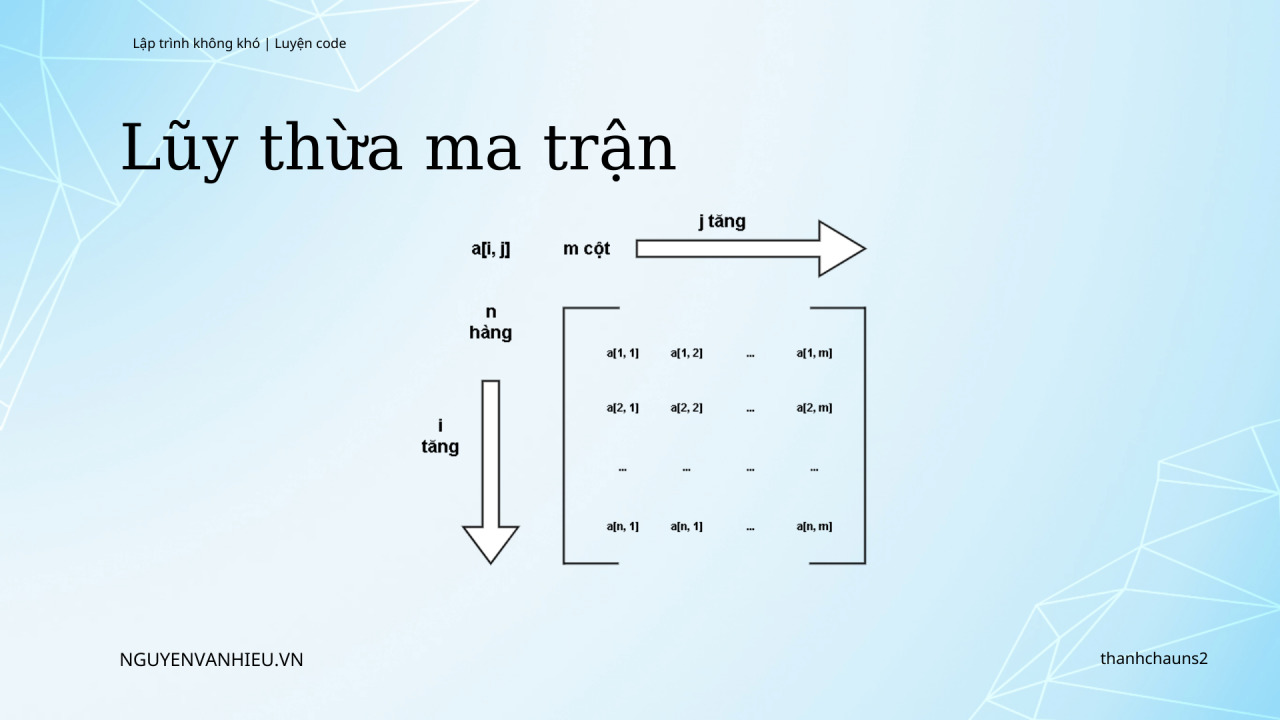
Khi các ma trận có cùng kích thước (chúng có cùng số hàng và cùng số cột) thì có thể thực hiện phép cộng hoặc trừ hai ma trận trên các phần tử tương ứng của chúng.
Tuy vậy, quy tắc áp dụng cho phép nhân ma trận chỉ có thể thực hiện được khi ma trận thứ nhất có số cột bằng số hàng của ma trận thứ hai:
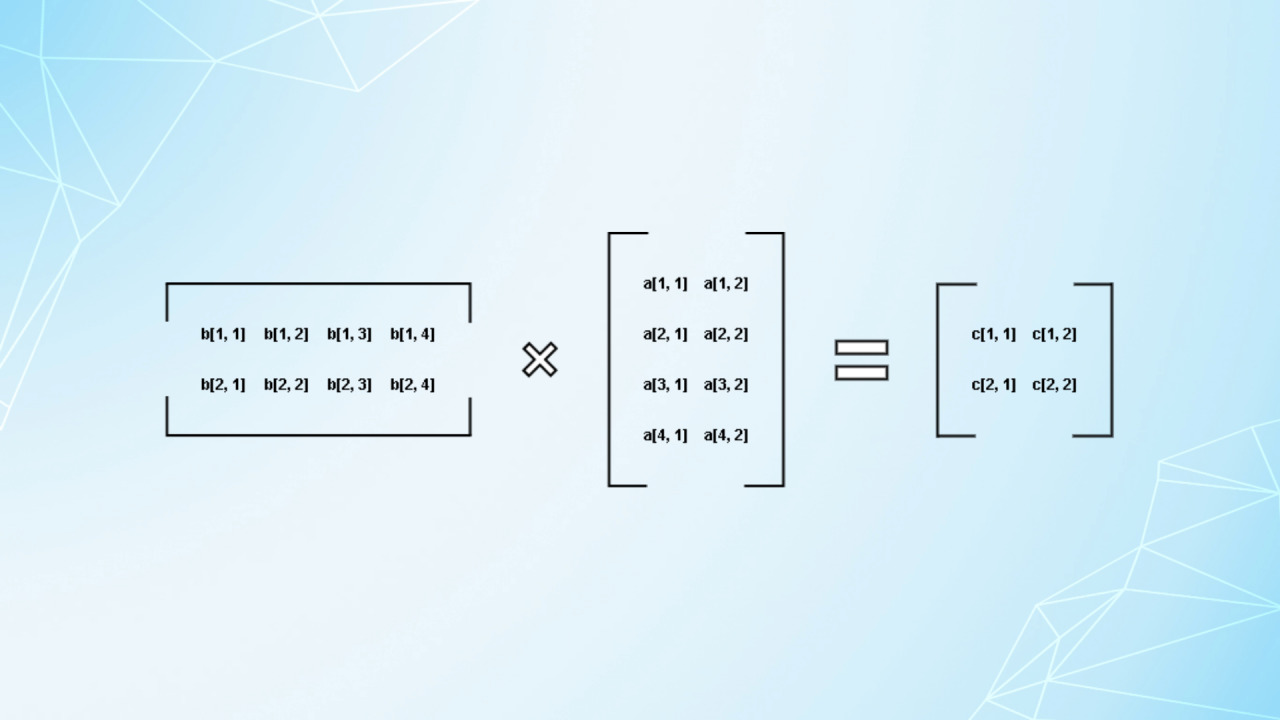
Với mỗi phần tử của ma trận đích được tính theo công thức: [latex]c[i, j] = sum_{x = 1}^{n}a[i, x] times b[x, j][/latex] với [latex]n[/latex] là chiều rộng của ma trận [latex]a[/latex]. Nói đơn giản thì, phần tử ô [latex][i, j][/latex] của ma trận kết quả là tổng của lần lượt các tích đôi một phần tử hàng [latex]i[/latex] của ma trận thứ nhất và cột [latex]j[/latex] của ma trận thứ hai.
Chú ý: Với hai ma trận A và B, [latex]A times B neq B times A[/latex]
Xét ví dụ nhân một ma trận 3×2 và một ma trận 2×4:
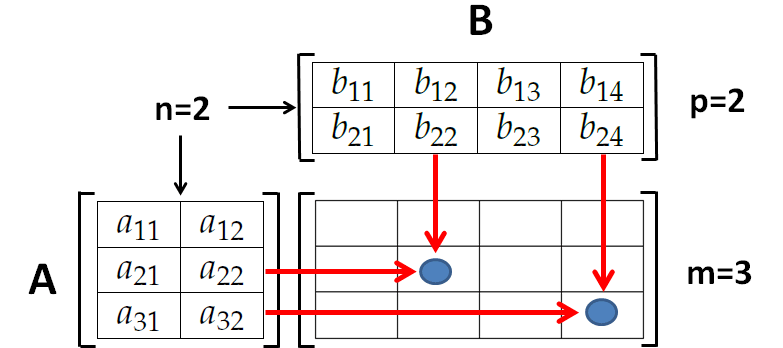Cho ma trận A kích thước 3×2 như sau:
1 2 2 3 2 5
Và một ma trận B kích thước 2×4:
1 2 3 4 1 3 5 7
Gọi ma trận kết quả của [latex]A times B[/latex] là C. Ma trận kết quả sẽ có số hàng bằng số hàng của ma trận đầu tiên và số cột bằng số cột của ma trận thứ hai, nên C sẽ có kích thước là 3×4.
Các phần tử của C sẽ được tính toán như sau:
C[1][1] = A[1][1] * B[1][1] + A[1][2] * B[2][1] = 1 * 1 + 2 * 1 = 1 + 2 = 3 C[1][2] = A[1][1] * B[1][2] + A[1][2] * B[2][2] = 1 * 2 + 2 * 3 = 2 + 6 = 8 C[1][3] = A[1][1] * B[1][3] + A[1][2] * B[2][3] = 1 * 3 + 2 * 5 = 3 + 10 = 13 C[1][4] = A[1][1] * B[1][4] + A[1][2] * B[2][4] = 1 * 4 + 2 * 7 = 4 + 14 = 18 C[2][1] = A[2][1] * B[1][1] + A[2][2] * B[2][1] = 2 * 1 + 3 * 1 = 2 + 3 = 5 C[2][2] = A[2][1] * B[1][2] + A[2][2] * B[2][2] = 2 * 2 + 3 * 3 = 4 + 9 = 13 C[2][3] = A[2][1] * B[1][3] + A[2][2] * B[2][3] = 2 * 3 + 3 * 5 = 6 + 15 = 21 C[2][4] = A[2][1] * B[1][4] + A[2][2] * B[2][4] = 2 * 4 + 3 * 7 = 8 + 21 = 29 C[3][1] = A[3][1] * B[1][1] + A[3][2] * B[2][1] = 2 * 1 + 5 * 1 = 2 + 5 = 7 C[3][2] = A[3][1] * B[1][2] + A[3][2] * B[2][2] = 2 * 2 + 5 * 3 = 4 + 15 = 19 C[3][3] = A[3][1] * B[1][3] + A[3][2] * B[2][3] = 2 * 3 + 5 * 5 = 6 + 25 = 31 C[3][4] = A[3][1] * B[1][4] + A[3][2] * B[2][4] = 2 * 4 + 5 * 7 = 8 + 35 = 43
Code minh họa cho ví dụ trên (Lưu ý từ khóa auto chỉ có từ C++11 hoặc mới hơn):
#include <iostream> // std::cin, std::cout
#include <vector> // std::vector
#define matrix std::vector<std::vector<int> >
matrix matrix_multiply(matrix a, matrix b) // Hàm nhân ma trận
{
int m = a.size(); // Lấy kích thước của 2 ma trận, ma trận a có kích thước m * n, ma trận b có kích thước n * k
int n = a[0].size();
int k = b[0].size();
matrix c(m, std::vector<int> (k)); // Ma trận kết quả c có kích thước m * k
for (int i = 0; i < m; i++) // Duyệt theo từng hàng của ma trận kết quả
{
for (int j = 0; j < k; j++) // Duyệt theo phần tử của mỗi hàng
{
c[i][j] = 0; // Đưa giá trị ban đầu về 0
for (int k = 0; k < n; k++) // Cộng kết quả mỗi lần nhân vào các phần tử
{
c[i][j] += a[i][k] * b[k][j];
}
}
}
return c;
}
int main() // C++11 required
{
matrix a = {
{1, 2},
{2, 3},
{2, 5}
};
matrix b = {
{1, 2, 3, 4},
{1, 3, 5, 7}
};
matrix c = matrix_multiply(a, b);
for (auto x : c) // In ra ma trận
{
for (auto y : x) std::cout << y << ' ';
std::cout << 'n';
}
}Kết quả chạy chương trình:
3 8 13 18 5 13 21 29 7 19 31 43
Phép lũy thừa ma trận
Tương tự với số nguyên, kết quả phép lũy thừa bậc n của một ma trận x là ma trận thu được khi nhân x với chính nó n lần.
Lưu ý: Chỉ ma trận vuông mới có thể thực hiện phép lũy thừa.
Code lũy thừa một ma trận (C++11):
#include <iostream>
#include <vector>
#define matrix std::vector<std::vector<int>>
matrix matrix_multiply(matrix a, matrix b) // Hàm nhân ma trận
{
int m = a.size(); // Lấy chiều dài 1 cạnh của ma trận, do các ma trận mà ma trận vuông cùng kích thước nên ta chỉ cần 1 độ dài 1 cạnh là đủ
matrix c(m, std::vector<int> (m)); // Khởi tạo ma trận kết quả
for (int i = 0; i < m; i++) // Nhân ma trận
{
for (int j = 0; j < m; j++)
{
c[i][j] = 0; // Đưa phần tử của ma trận kết quả về 0
for (int k = 0; k < m; k++) // Cộng đáp án vào kết quả
{
c[i][j] += a[i][k] * b[k][j];
}
}
}
return c;
}
matrix power(matrix a, int b) // Lũy thừa ma trận
{
if (b == 1) return a;
else return matrix_multiply(a, power(a, b - 1));
}
int main(){
matrix a = {
{1, 2},
{2, 3}
};
int n = 2;
matrix c = power(a, n);
for (auto x : c) // In ra ma trận
{
for (auto y : x) std::cout << y << ' ';
std::cout << 'n';
}
}Kết quả chạy chương trình:
5 8 8 13
Tìm số Fibonacci thứ N
Một trong những ứng dụng rộng rãi nhất của lũy thừa ma trận đó là để tìm số Fibonacci thứ n. Để tìm 1 số Fibonacci, chúng ta có thể dựa vào quy luật sau:
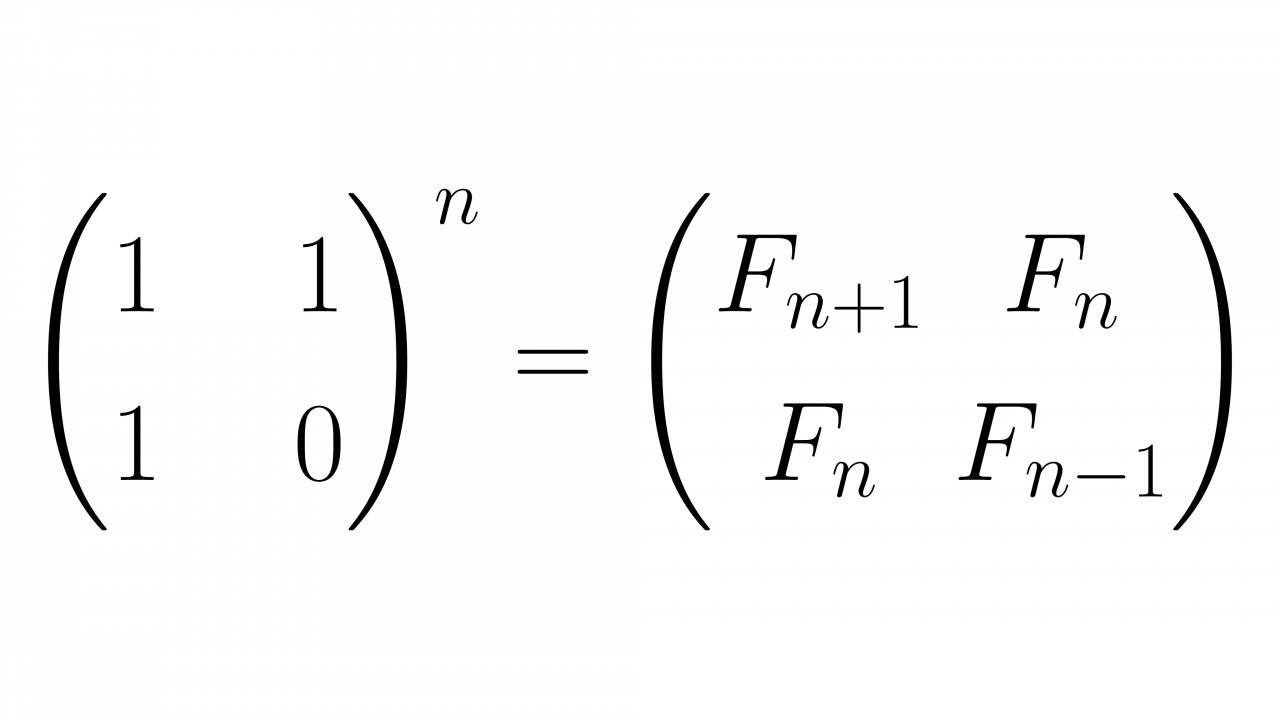
Với [latex]F(1)=1, F(2) = 1[/latex]
Chương trình sử dụng lũy thừa ma trận để tính số Fibonacci thứ n (C++ 11):
#include <iostream> // std::cin, std::cout, std::endl
#include <vector> // std:: vector
#define matrix std::vector<std::vector<int>>
matrix matrix_multiply(matrix a, matrix b) // Hàm nhân ma trận
{
int m = a.size(); // Chiều dài 1 cạnh của ma trận
matrix c(m, std::vector<int> (m)); // Khởi tạo ma trận kết quả
for (int i = 0; i < m; i++) // Nhân ma trận
{
for (int j = 0; j < m; j++)
{
c[i][j] = 0; // Đưa phần tử ma trận kết quả về 0 trước khi tính toán
for (int k = 0; k < m; k++) // Cộng vào kết quả
{
c[i][j] += a[i][k] * b[k][j];
}
}
}
return c;
}
matrix power(matrix a, int b) // Lũy thừa ma trận
{
if (b == 1) return a; // Nếu số mũ bằng 1 thì trả về a
else return matrix_multiply(a, power(a, b - 1)); // Nếu không thì trả về a * a ^ (b - 1)
}
int main() // C++11 required
{
matrix fibonacci = { // Ma trận gốc để tìm số fibonacci
{1, 1},
{1, 0}
};
std::cout << "Nhap so Fibonacci ma ban muon tim kiem: ";
int n; // Số mũ lũy thừa
std::cin >> n;
matrix answer = power(fibonacci, n); // Tiến hành tìm đáp án
std::cout << "So Fibonacci thu " << n << " la: " << answer[1][0] << std::endl; // In ra kết quả
}Giả sử [latex]n = 4[/latex], đây là output của chương trình:
Nhap so Fibonacci ma ban muon tim kiem: 4 So Fibonacci thu 4 la: 3
Để lại một bình luận