Ở bài này, mình sẽ hướng dẫn các bạn cách để “xóa Node – Deletion” trong cây AVL. Và đây cũng là phần cuối của series AVL Tree. Bởi lẽ bản chất của AVL Tree chính là BST (Binary Search Tree) ở dạng cân bằng, do đó ngoài Insert và Delete ra thì các hàm còn lại như search, findMax, print, … viết hoàn toàn giống với hàm của BST.
1. Kiến thức cần nắm
Như đã nói, cây AVL bản chất là cây tìm kiếm nhị phân – BST ở dạng cân bằng. Vì vậy nếu bạn muốn xóa Node ở cây AVL thì phải nắm rõ kiến thức dưới đây. Còn nếu bạn vẫn còn lơ mơ thì hãy đọc lại cho hiểu nhé.
- Cách xóa một Node trong cây BST (Cây tìm kiếm nhị phân)
- Các trường hợp cây lệch và cách xử lý (AVL Tree – P1 Insertion)
2. Chuyện gì xảy ra nếu xóa một Node?
Chúng ta sẽ xóa một Node của cây AVL giống y như cây BST. Như vậy, sẽ có 3 trường hợp chính đó là:
- Node có 0 con (Node lá): Mình chỉ cần giải phóng bộ nhớ Node đó là xong.
- Node chỉ có 1 con: Giải phóng Node đó rồi thay bởi Node con.
- Node có 2 con: Tìm Node con nhỏ nhất bên phải hoặc lớn nhất bên trái (gọi là temp) rồi gán giá trị Node này cho Node cần xóa sau đó xóa temp. Temp là Node nhỏ nhất (lớn nhất) nên chỉ có thể có 1 hoặc 0 con => Xóa như 2 TH trên.
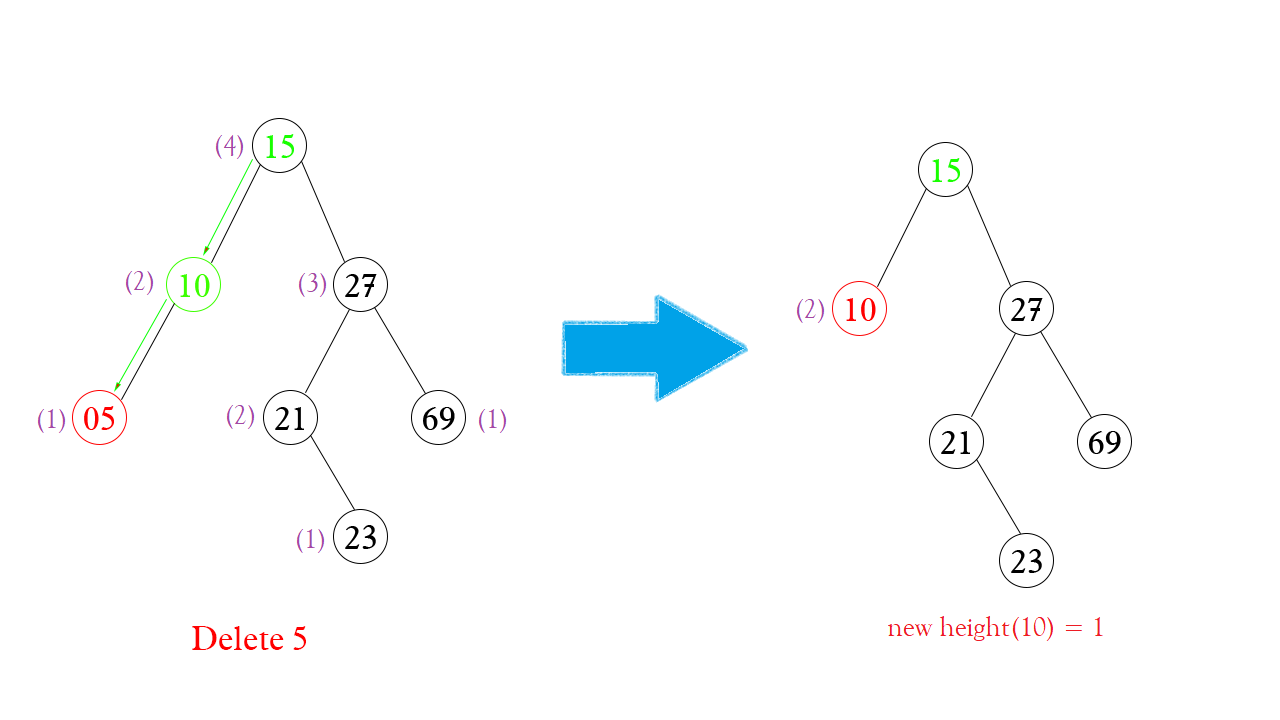
Có thể thấy rằng: khi xóa Node 5 thì cây đã không còn cân bằng (lệch phải), như vậy thì đây không phải là cây AVL nữa. Và ngoài ra nếu để ý kĩ thì chiều cao của Node 10 vẫn là (2) trong khi đúng ra phải là (1).
Vậy sau khi xóa Node trên cây AVL ta phải làm 2 việc sau:
- Cập nhật lại chiều cao.
- Xử lý các trường hợp cây bị lệch.
3. Cập nhật chiều cao
Chúng ta sẽ sử dụng đệ quy để duyệt cây, nhằm tìm ra Node cần xóa. Ví dụ cần xóa Node 21 thì duyệt cây như sau:
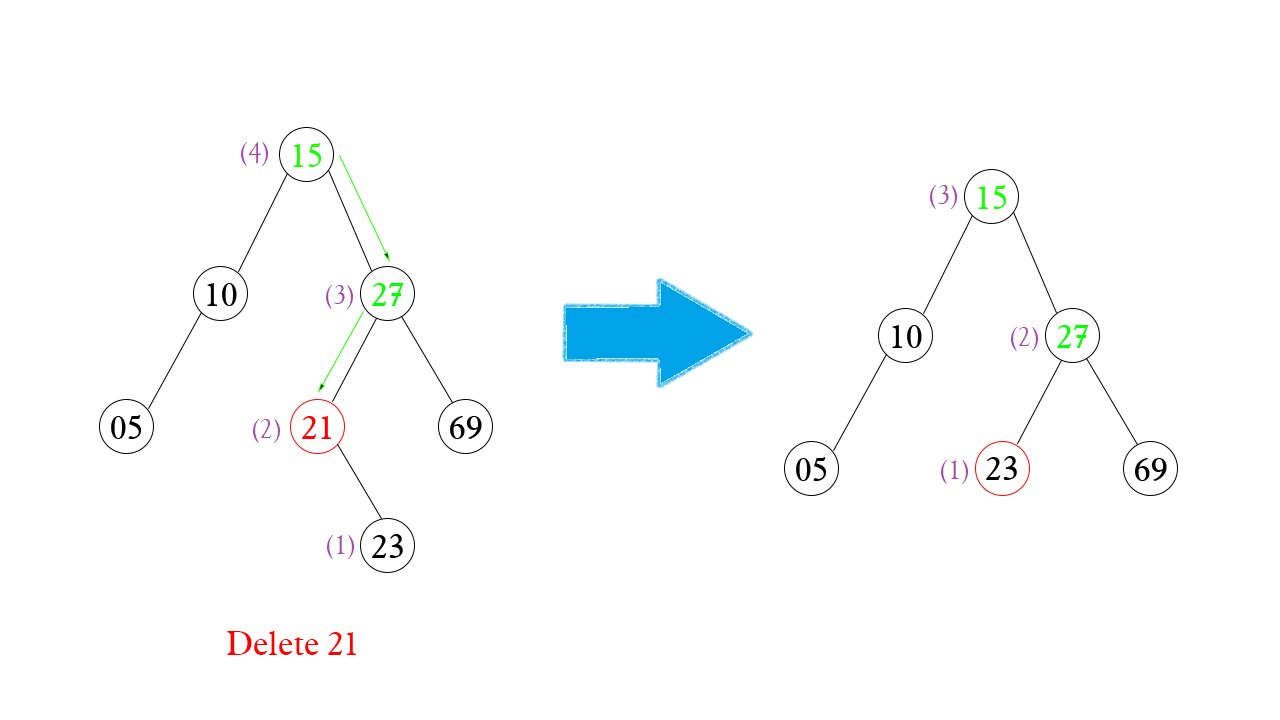
Có thể thấy, chỉ có các Node nằm trên đường duyệt (xanh lá) mới bị thay đổi về chiều cao. Vậy làm sao để cập nhật lại chiều cao cho các Node đó?
Rất may là vì khi sử dụng đệ quy (recursive) thì chúng ta đã duyệt qua các Node ấy rồi. Nên sau khi xóa thì chỉ cần cập nhật chiều cao một lần là xong.
Node* deleteNode(Node* root, int key) {
if (root == NULL)
return root;
if (key > root->data)
root->right = deleteNode(root->right, key);
else if (key < root->data)
root->left = deleteNode(root->left, key);
// Nếu key có giá trị bằng với root->data
// Thì đây chính là Node cần xóa
else {
// Delete
}
// Nếu không còn gì thì trả về luôn !!
if (root == NULL)
return root;
// CẬP NHẬT CHIỀU CAO - UPDATE HEIGHT
root->height = 1 + max(getHeight(root->left), getHeight(root->right));
}
4. Xử lý các trường hợp cây bị lệch.
Ở bài trước, chúng ta đã biết được 4 trường hợp cây bị lệch. Đó là: Trái trái, Trái phải, Phải phải, Phải trái. Về tổng quan (Trái/Phải) thì có biết được cây lệch về phía nào qua giá trị cân bằng. Còn về chi tiết (trái/phải) thì phải kiểm tra qua Node vừa được thêm vào (Insert). Tuy nhiên, lần này là xóa nên không thể làm như trước.
0. Giá trị cân bằng – Value Balance
Vậy để biết được phần chi tiết như thế nào thì chỉ còn cách tính giá trị cân bằng (Value Balance). Mình sẽ viết một hàm kiểm tra giá trị cân bằng để sử dụng nhiều lần.
int valueBalance(Node* root) {
if (root == NULL)
return 0;
return getHeight(root->left) - getHeight(root->right);
}
1. Trường hợp cây lệch Trái – Left case
Gọi Node x, y lần lượt là con trái phải của root. Rõ ràng cây bị lệch sang trái khi:
height(x) – height(y) > 1 hay valueBalance(root) > 1
Bây giờ, hãy kiểm tra chi tiết cây lệch qua hướng nào thông qua Node x để xem là trường hợp Trái trái hay Trái phải (Left left or Left right).
a. valueBalance(x) > 0
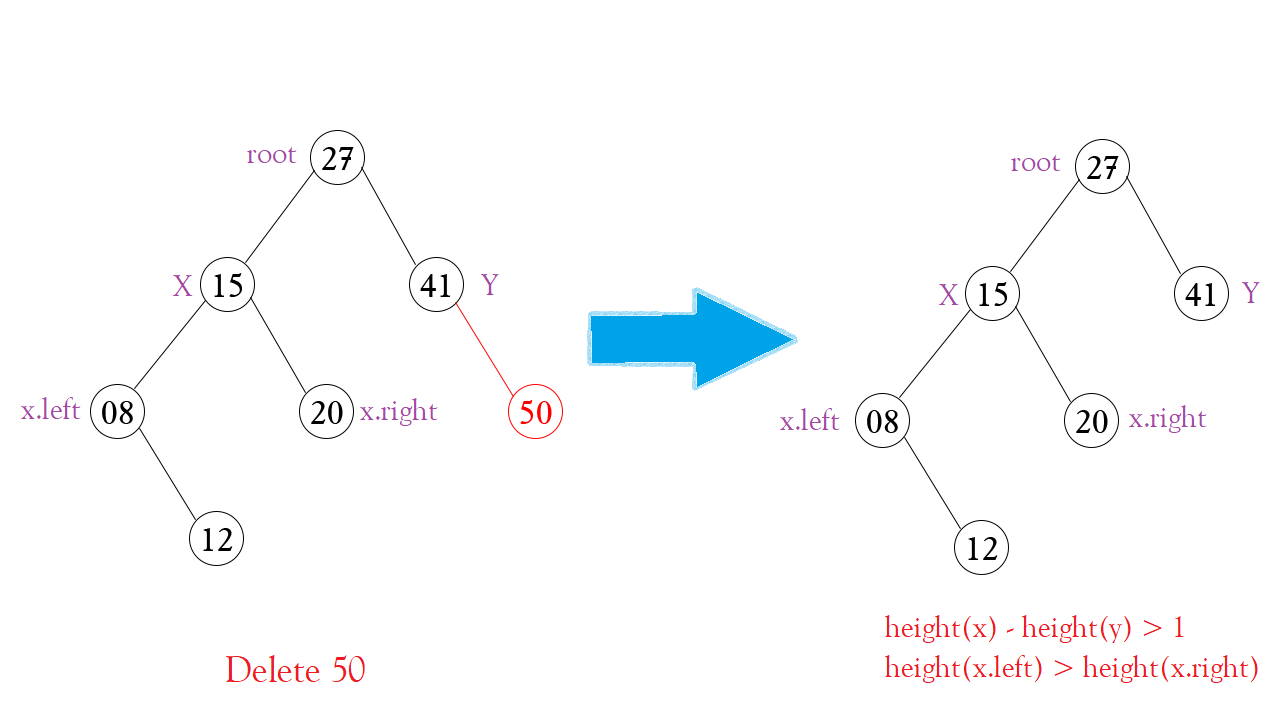
Rõ ràng, khi height(x.left) > height(x.right) thì đây chính là trường hợp Trái trái – Left left
b. valueBalance(x) < 0
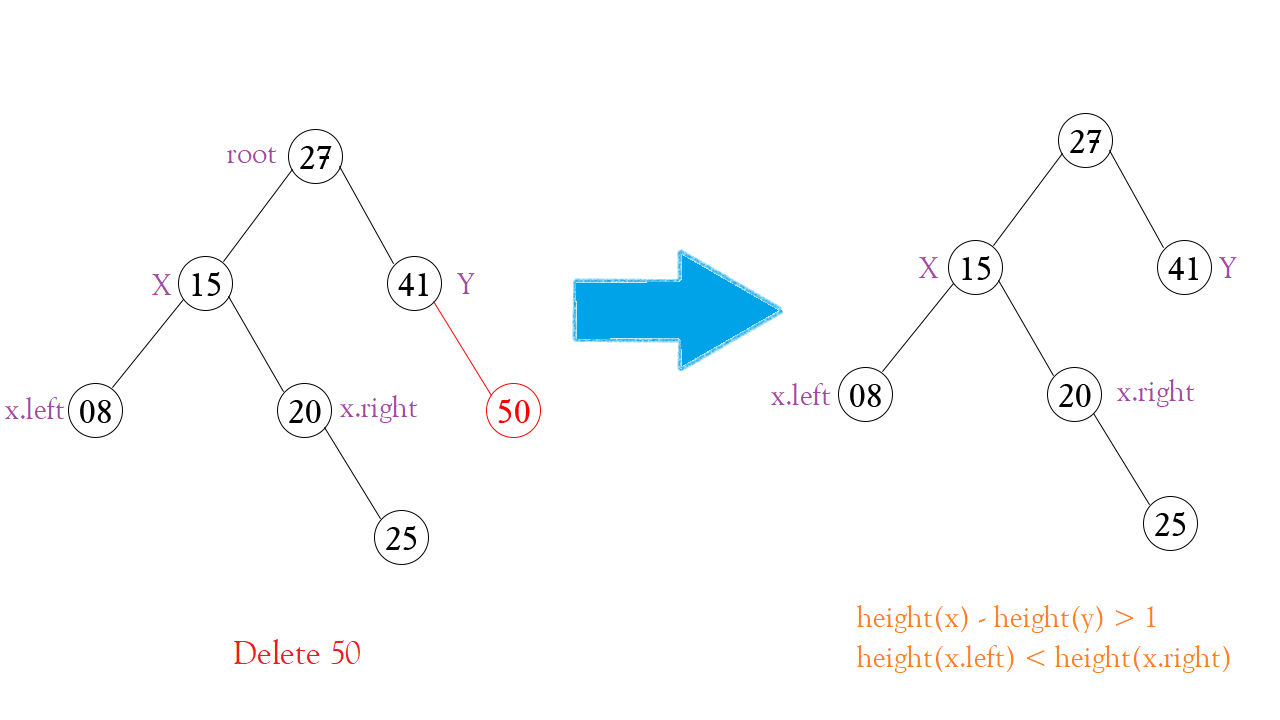
Hiển nhiên, khi height(x.left) < height(x.right) thì đây chính là trường hợp Trái phải – Left right
c. valueBalance(x) = 0
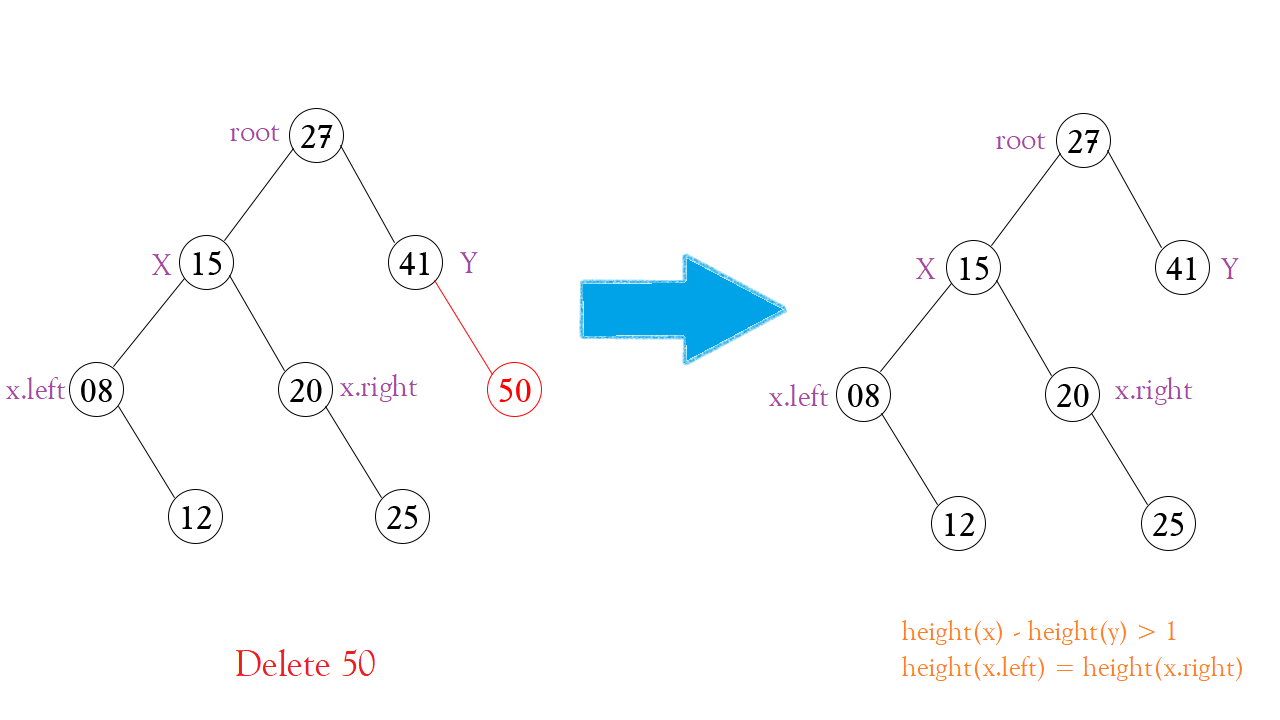
Có thể thấy: cây con X đã cân bằng (height(x.left) = height(x.right)) do đó ta chỉ cần quay phải (rotate right) Node root là xong.
Vì thế nên trường hợp này được tính vào Trái trái – Left left
d. Kết luận
Trường hợp Trái trái – Left left:
Xảy ra khi: valueBalance(root) > 1 && valueBalance(x) >= 0
Xử lí: quay phải Node root – rightRotate(root)
Trường hợp Trái phải – Left right:
Xảy ra khi: valueBalance(root) > 1 && valueBalance(x) < 0
Xử lí: leftRotate(x) => rightRotate(root)
2. Trường hợp cây lệch Phải – Right case
Hoàn toàn tương tự, các bạn có thể tự vẽ ra ở giấy để hiểu bài hơn nhé. Gọi x và y lần lượt là Node trái và phải của root. Ta có:
Trường hợp Phải phải- Right right:
Xảy ra khi: valueBalance(root) < -1 && valueBalance(y) <= 0
Xử lí: quay trái Node root – leftRotate(root)
Trường hợp Phải trái – Right left:
Xảy ra khi: valueBalance(root) < -1 && valueBalance(y) > 0
Xử lí: rightRotate(y) => leftRotate(root)
5. Code chính – Insert + Delete
#include <iostream>
#include <cmath>
#define COUNT 10
using namespace std;
struct Node {
int data;
Node* left;
Node* right;
int height;
};
int getHeight(Node* root) {
if (root == NULL)
return 0;
//return 1 + max(getHeight(root->left), getHeight(root->right));
return root->height;
}
Node* rightRotate(Node* root){
Node* x = root->left;
// Bắt đầu quay phải
root->left = x->right;
x->right = root;
// Thiết lập chiều cao
root->height = 1 + max(getHeight(root->left), getHeight(root->right));
x->height = 1 + max(getHeight(x->left), getHeight(x->right));
// Return x - trả về root mới
return x;
}
Node* leftRotate(Node* root) {
Node* y = root->right;
// Bắt đầu quay trái
root->right = y->left;
y->left = root;
// Thiết lập chiều cao
root->height = 1 + max(getHeight(root->left), getHeight(root->right));
y->height = 1 + max(getHeight(y->left), getHeight(y->right));
// Return y - trả về root mới
return y;
}
// Insertion - AVL Tree
Node* Insert(Node* root, int value) {
// 1. Insert
if (root == NULL)
return new Node{ value, NULL, NULL, 1 }; // Trả về Node có height = 1
if (value > root->data)
root->right = Insert(root->right, value);
else if (value < root->data)
root->left = Insert(root->left, value);
else
return root; // Neu bang thi khong them
// 2. Set height
root->height = 1 + max(getHeight(root->left), getHeight(root->right));
// 3. Rotate
int valBalance = getHeight(root->left) - getHeight(root->right);
// Kiểm tra 4 TH xảy ra:
// 4.1. Left left
if (valBalance > 1 && value < root->left->data)
return rightRotate(root);
// 4.2. Right Right
if (valBalance < -1 && value > root->right->data)
return leftRotate(root);
// 4.3. Left Right
if (valBalance > 1 && value > root->left->data) {
root->left = leftRotate(root->left);
return rightRotate(root);
}
// 4.4. Right Left
if (valBalance < -1 && value < root->right->data) {
root->right = rightRotate(root->right);
return leftRotate(root);
}
return root;
}
// Giá trị cân bằng - Value Balance
int valueBalance(Node* root) {
if (root == NULL)
return 0;
return getHeight(root->left) - getHeight(root->right);
}
Node* maxValueNode(Node* root)
{
Node* current = root;
// Tìm kiếm Node có giá trị lớn nhất
while (current->right != NULL)
current = current->right;
return current;
}
// Deletion - AVL Tree
Node* deleteNode(Node* root, int key) {
// 1. XÓA NODE - DELETE
if (root == NULL)
return root;
if (key > root->data)
root->right = deleteNode(root->right, key);
else if (key < root->data)
root->left = deleteNode(root->left, key);
// Nếu key có giá trị bằng với root->data
// Thì đây chính là Node cần xóa
else {
// Trường hợp 0 con hoặc 1 con
if (root->left == NULL || root->right == NULL) {
// Sử dụng Node temp để kiểm tra
Node* temp = root->left;
if (root->right != NULL)
temp = root->right;
// TH: 0 con - No child case
if (temp == NULL) {
temp = root;
root = NULL;
delete temp;
}
// TH: 1 con - One child case
else {
// Gán tất cả các giá trị (bao gồm left, right, height) của temp vào root
*root = *temp;
delete temp;
}
}
// Trường hợp 2 con - Two child case
else {
// Tìm Node lớn nhất bên trái (nhỏ nhất bên phải)
// successor - biggest in the left subtree
Node* temp = maxValueNode(root->left);
// Đưa data của temp vào root
root->data = temp->data;
// Xóa temp như 2 TH trên - Delete the inorder successor
root->right = deleteNode(root->right, temp->data);
}
}
// Nếu không còn gì thì trả về luôn !!
if (root == NULL)
return root;
// 2. CẬP NHẬT CHIỀU CAO - UPDATE HEIGHT OF THE CURRENT NODE
root->height = 1 + max(getHeight (root->left), getHeight (root->right));
// 3. CÂN BẰNG CÂY - GET THE BALANCE FACTOR
int valBalance = valueBalance(root);
// Kiểm tra 4 TH xảy ra - There are 4 cases
// Case 1: Left left - Trái trái
if (valBalance > 1 && valueBalance(root->left) >= 0)
return rightRotate(root);
// Case 2: Right right - Phải phải
if (valBalance < -1 && valueBalance(root->right) <= 0)
return leftRotate(root);
// Case 3: Left right - Trái phải
if (valBalance > 1 && valueBalance(root->left) < 0){
root->left = leftRotate(root->left);
return rightRotate(root);
}
// Case 4: Right left - Phải trái
if (valBalance < -1 && valueBalance(root->right) > 0){
root->right = rightRotate(root->right);
return leftRotate(root);
}
return root;
}
// In - Print 2D ra console
void print2DUtil(Node* root, int space){
if (root == NULL)
return;
space += COUNT;
print2DUtil(root->right, space);
cout << endl;
for (int i = COUNT; i < space; i++)
cout << " ";
cout << root->data << " (" << root->height << ") " << "n";
print2DUtil(root->left, space);
}
void print2D(Node* root){
print2DUtil(root, 0);
}
int main() {
Node* tree = NULL;
tree = Insert(tree, 10);
tree = Insert(tree, 5);
tree = Insert(tree, 15);
tree = Insert(tree, 3);
tree = Insert(tree, 12);
tree = Insert(tree, 17);
tree = Insert(tree, 11);
print2D(tree);
cout << "n ------------Delete 3----------- n";
tree = deleteNode(tree, 3);
print2D(tree);
}Kết quả console
17 (1)
15 (3)
12 (2)
11 (1)
10 (4)
5 (2)
3 (1)
------------Delete 3-----------
17 (1)
15 (2)
12 (3)
11 (1)
10 (2)
5 (1)
Cảm ơn các bạn đã đọc, mình xin kết thúc series AVL Tree tại đây. Nếu thấy Nếu thấy hay thì hãy chia sẽ nó cho mọi người cùng đọc nhé ! Ngoài ra, bạn nào muốn tham khảo code các ngôn ngữ khác thì hãy truy cập vào Geeks for geeks – AVL Tree – Set 2
Thân mến.
Để lại một bình luận