Cây AVL (tiếng Anh là AVL Tree, AVL là viết tắt tên của các tác giả phát minh ra nó Adelson-Velsky và Landis). Cây AVL là một cây tìm kiếm nhị phân có khả năng tự cân bằng, điều đó giúp cho cây AVL tối ưu hơn rất nhiều so với cây tìm kiếm nhị phân (vd. Cây tìm kiếm nhị phân của dãy số tăng dần và node gốc là phần tử đầu tiên). Chúng ta hãy cùng đi tìm hiểu về AVL tree (phần 1 – Insertion) trong bài viết này nhé.
1. Tại sao lại sử dụng cây AVL?
Cây AVL chính sự nâng cấp của cây BST (Binary Search Tree) nên nếu bạn chưa biết gì về cây BST thì hãy đọc bài viết cây tìm kiếm nhị phân này trước khi bắt đầu.
Vậy thì BST có điểm yếu gì mà phải nâng cấp, hãy cùng nhìn:
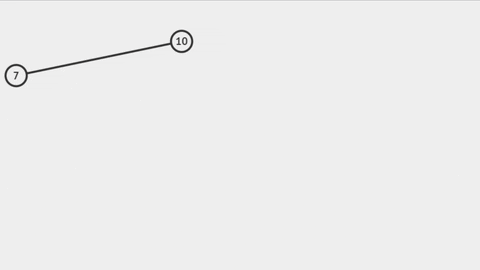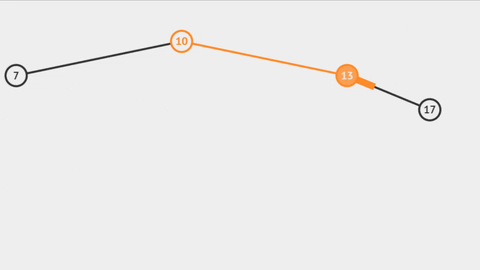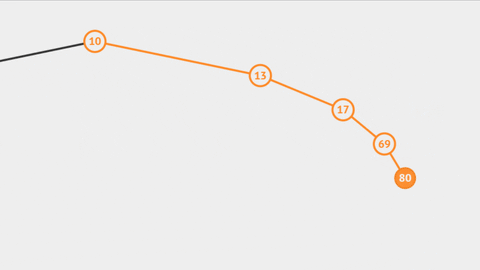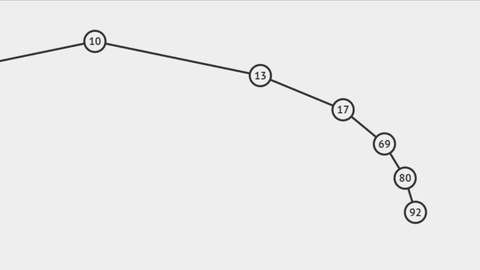
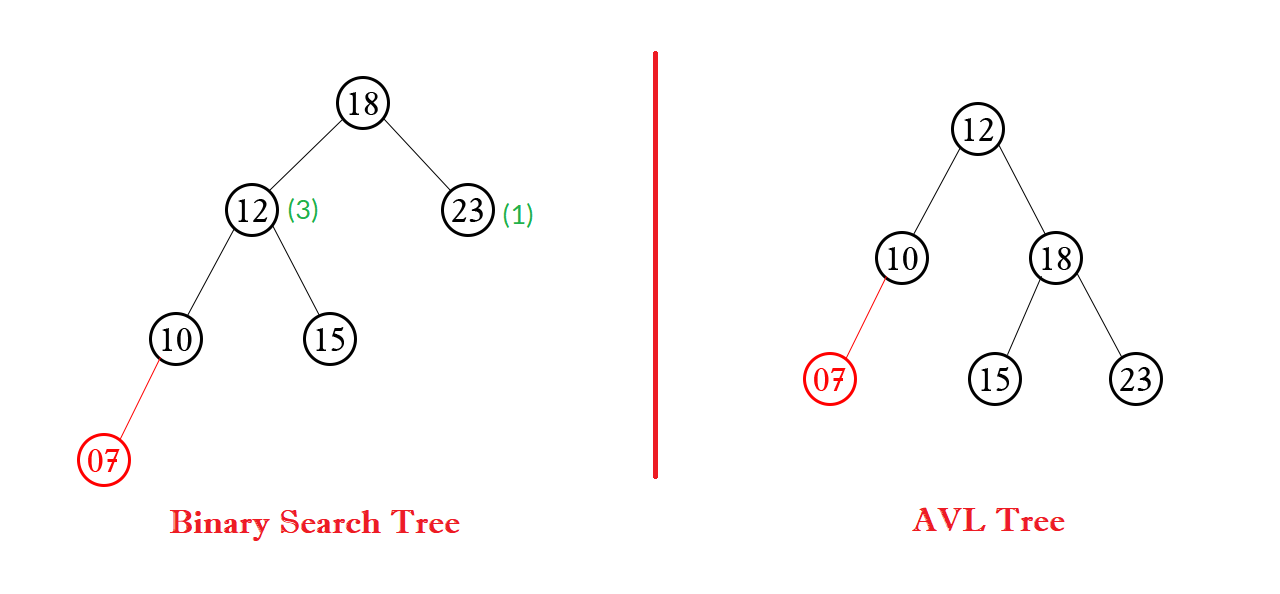
Có thể thấy rằng, khi ta thêm các phần tử theo thứ tự tăng dần (giảm dần) thì cây không khác gì một Linked List (Danh sách liên kết). Khi đó, độ phức tạp của thuật toán tìm kiếm của cây là O(n) chứ không phải O(log n). Như vậy, ưu điểm của BST so với Linked List coi như cũng không còn.
2. Cây AVL là gì?
Cây AVL là cây nhị phân tìm kiếm cân bằng với “chiều cao” giữa cây con bên trái và cây con bên phải chênh nhau không vượt quá 1. Hay nói cách khác, BST mà cây con bên trái và phải của mọi Node có “chiều cao” chênh lệch không vượt 1 thì chính là cây AVL.
Để xây dựng được cây AVL thì các bạn nắm rõ các yếu tố sau:
- Khái niệm “chiều cao” và cách tính.
- Các kỹ thuật quay cây AVL
- Các trường hợp cây bị lệch
3. Xây dựng cây AVL
a. Định nghĩa kiểu dữ liệu các Node
struct Node {
int data;
Node* left;
Node* right;
int height;
};b. Chiều cao của mỗi Node và cách tính
Chiều cao của một Node chính là số các node trên một đường dẫn dài nhất từ Node đó đến Node = NULL. Và quy ước Node = NULL có chiều cao bằng 0.
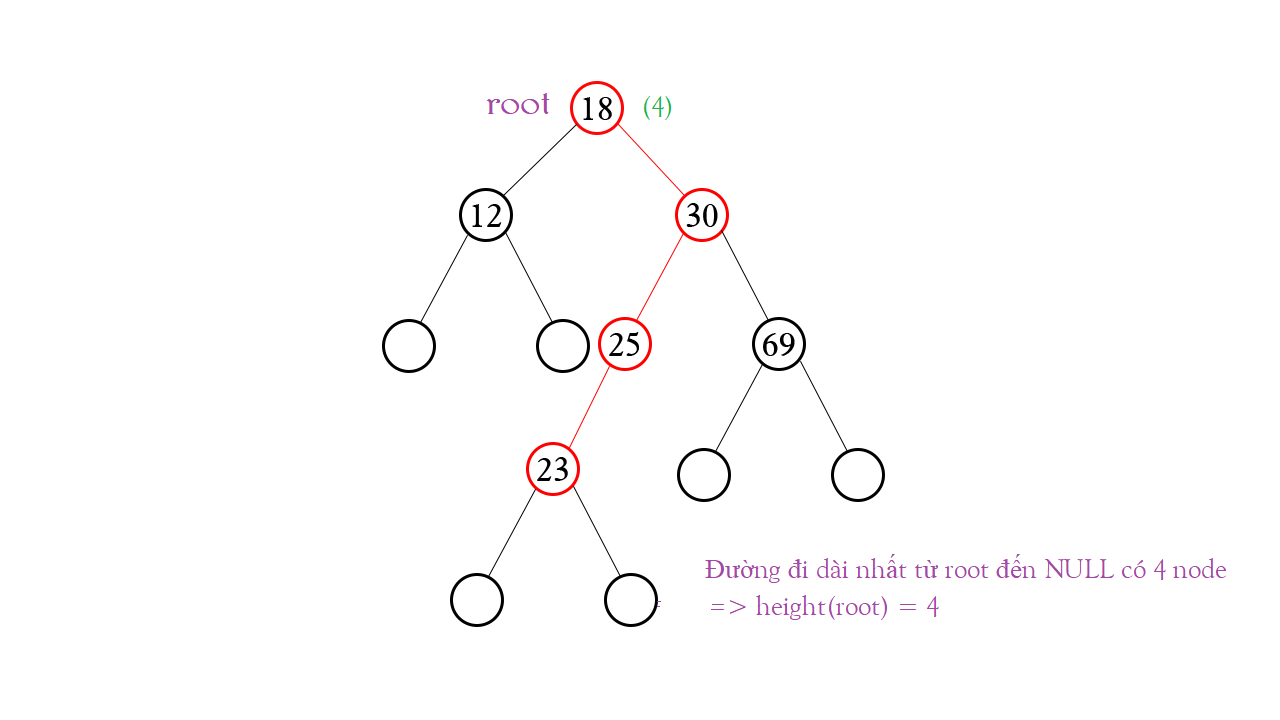Bạn có thể tính độ cao qua hàm đệ quy như cách dưới đây. Tuy nhiên, mình sẽ không áp dụng vào code chính bởi vì khi dữ liệu đầu vào cực lớn thì việc đệ quy để tính chiều cao một Node bằng cách dựa vào tất cả các Node con là rất mất thời gian.
int getHeight(Node* root) {
if (root == NULL)
return 0;
return 1 + max(getHeight(root->left), getHeight(root->right));
}c. Các kỹ thuật quay cây AVL
Có thể thấy cây BST khi không cân bằng sẽ bị lệch sang phía bên trái hoặc bên phải. Để điều chỉnh lại ta cần phải quay cây sang phía ngược lại.
i. Kỹ thuật quay phải – áp dụng khi cây bị lệch trái
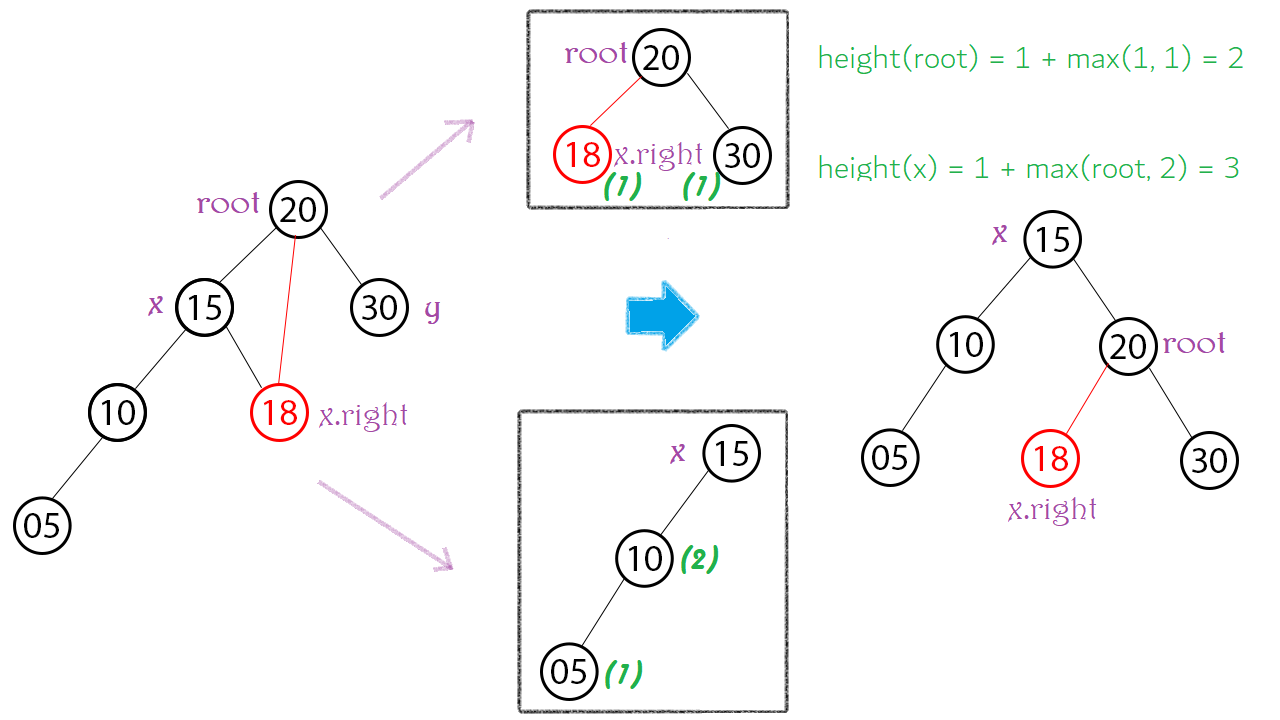
Gọi Node x, y lần lượt là các con trái, phải của root. Bây giờ, ta chỉ cần chú ý đến 3 Node: root, x, x.right.
Con trái của root không còn là x nữa mà là x.right hay root.left = x.right
X sẽ lên làm Node cha với con phải là root hay x.right = root
Về chiều cao, có thể thấy chỉ có 2 Node bị thay đổi chiều cao đó là root và x. Vì root là con của x nên phải tính chiều cao của root trước.
root.height = 1 + max(root.left, root.right)
x.height = 1 + max(x.left, x.right)
Node* rightRotate(Node* root){
Node* x = root->left;
// Bắt đầu quay phải
root->left = x->right;
x->right = root;
// Thiết lập chiều cao
root->height = 1 + max(getHeight(root->left), getHeight(root->right));
x->height = 1 + max(getHeight(x->left), getHeight(x->right));
// Return x - trả về root mới
return x;
}ii. Kỹ thuật quay trái – áp dụng khi cây bị lệch phải
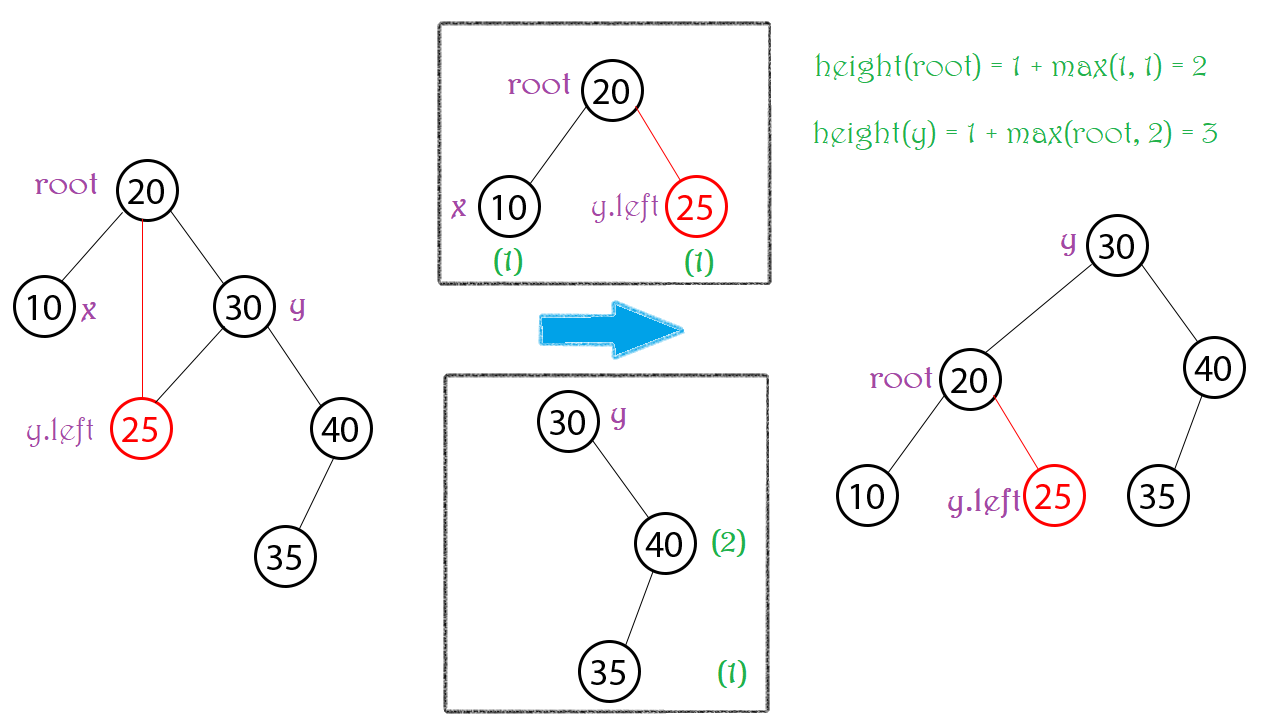
Hoàn toàn tương tự, gọi x y lần lượt là các con trái phải của root. Và ta chỉ cần quan tâm 3 Node: root, y, y.left
Node* leftRotate(Node* root) {
Node* y = root->right;
// Bắt đầu quay trái
root->right = y->left;
y->left = root;
// Thiết lập chiều cao
root->height = 1 + max(getHeight(root->left), getHeight(root->right));
y->height = 1 + max(getHeight(y->left), getHeight(y->right));
// Return y - trả về root mới
return y;
}4. Các trường hợp cây bị lệch
1. Trường hợp “Trái trái” – Left left
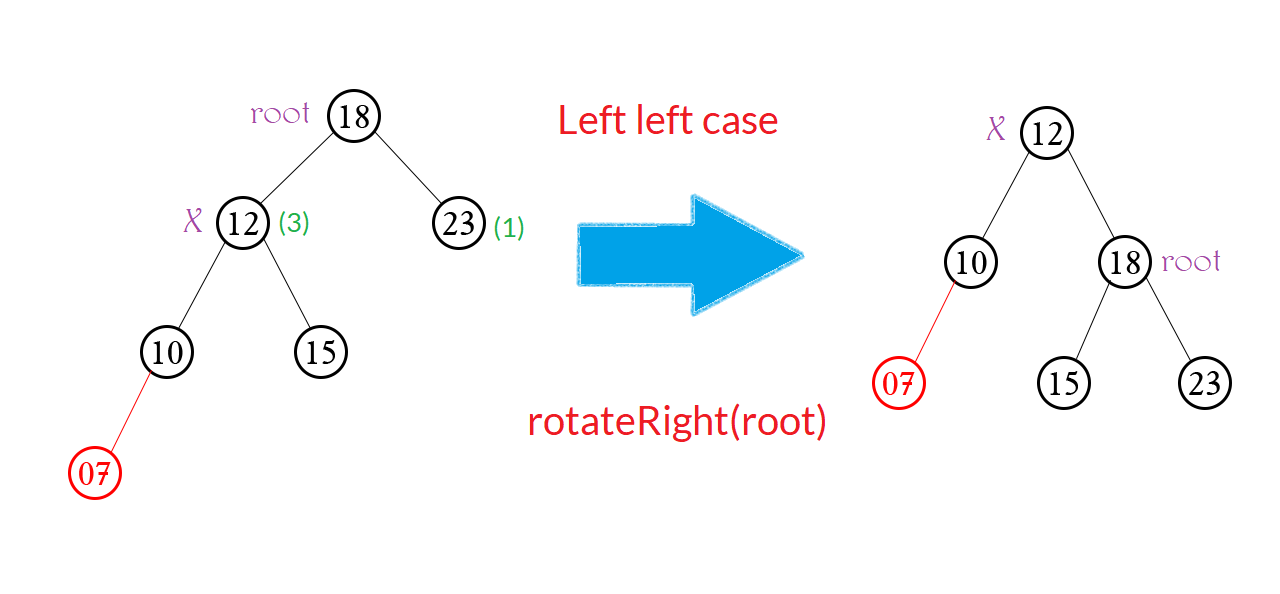Gọi Node X và Y lần lượt là con trái và con phải của root. Có thể thấy rằng chênh lệch về độ cao giữa X và Y là 3 – 1 = 2 nghiêng về cho x. Điều này nói lên rằng: cây bị lệch sang bên trái.
Tiếp tục, hãy nhìn vào Node màu đỏ vừa mới được thêm vào. Ta có thể thấy: Node đỏ nằm bên trái của Node X hay giá trị Node đỏ < giá trị Node X. Vì vậy nên trường hợp này mới có tên là “Trái trái“.
Tóm lại:
Xảy ra khi: height(X) – height(Y) > 1 và value(Đỏ) < value(X)
Xử lý: quay phải Node root – rotateRight(root)
2. Trường hợp “Trái phải” – Left right
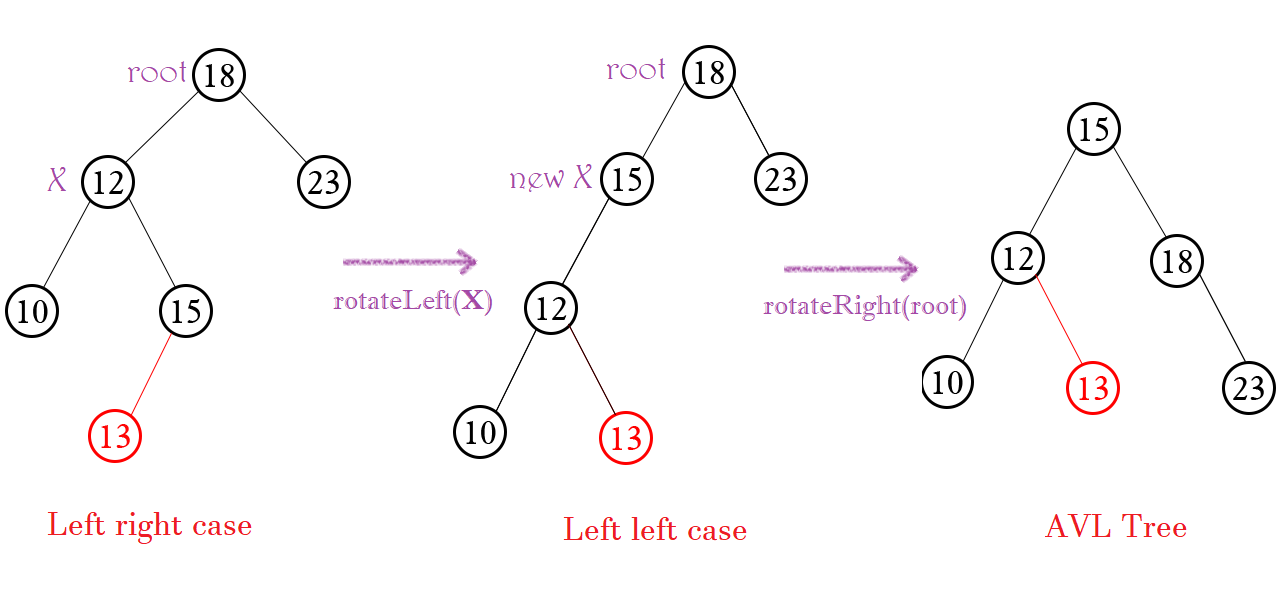Gọi Node X và Y lần lượt là con của root. Có thể thấy: cây đã bị lệch sang bên trái – khá giống với trường hợp trước. Tuy nhiên điểm khác chính là Node đỏ được thêm vào. Lần này Node đỏ nằm bên phải so với Node X.
Có thể tưởng tượng rằng: khi nhìn tổng quan cây, thì cây bị lệch sang bên trái; còn khi nhìn chi tiết bên trái, thì lại thấy cây nghiêng về bên phải một xíu.
Xử lý: Vì cây con X bị nghiêng sang phải nên chỉ cần quay trái X thì sẽ được trường hợp “Trái trái” như trước. Rồi sau đó quay phải root như trường hợp 1.
Tóm lại:
Xảy ra khi: height(X) – height(Y) > 1 và value(Đỏ) > value(X)
Xử lý: rotateLeft(X) -> rotateRight(root)
3. Trường hợp “Phải phải” – Right right
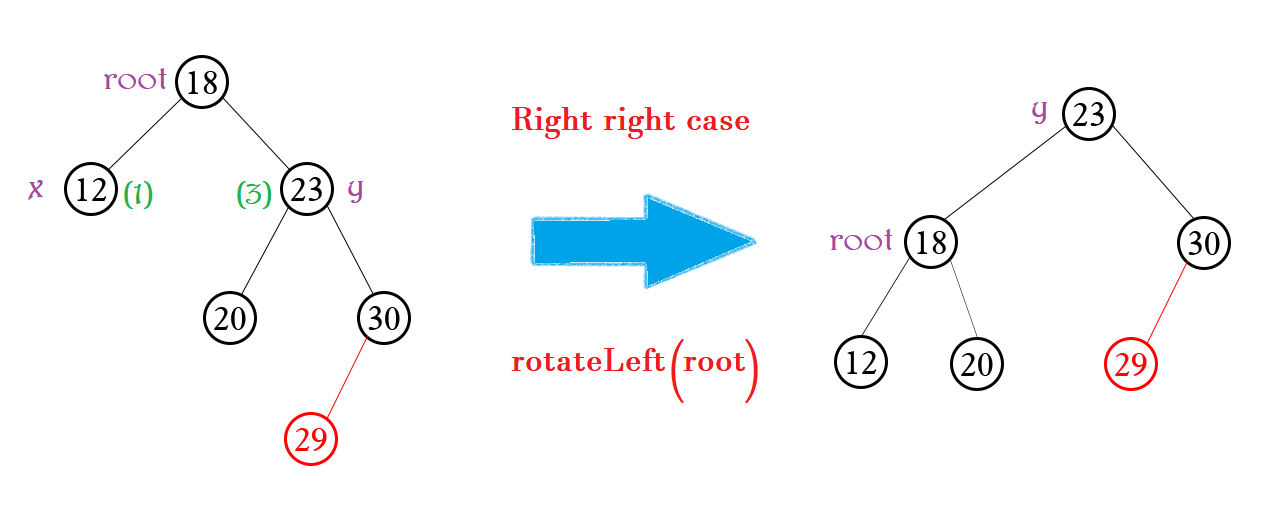
Hoàn toàn tương tự “Trái trái” – Left left
Xảy ra khi: height(X) – height(Y) < -1 và value(Đỏ) > value(Y)
Xử lý: rotateLeft(root)
4. Trường hợp “Phải trái” – Right left
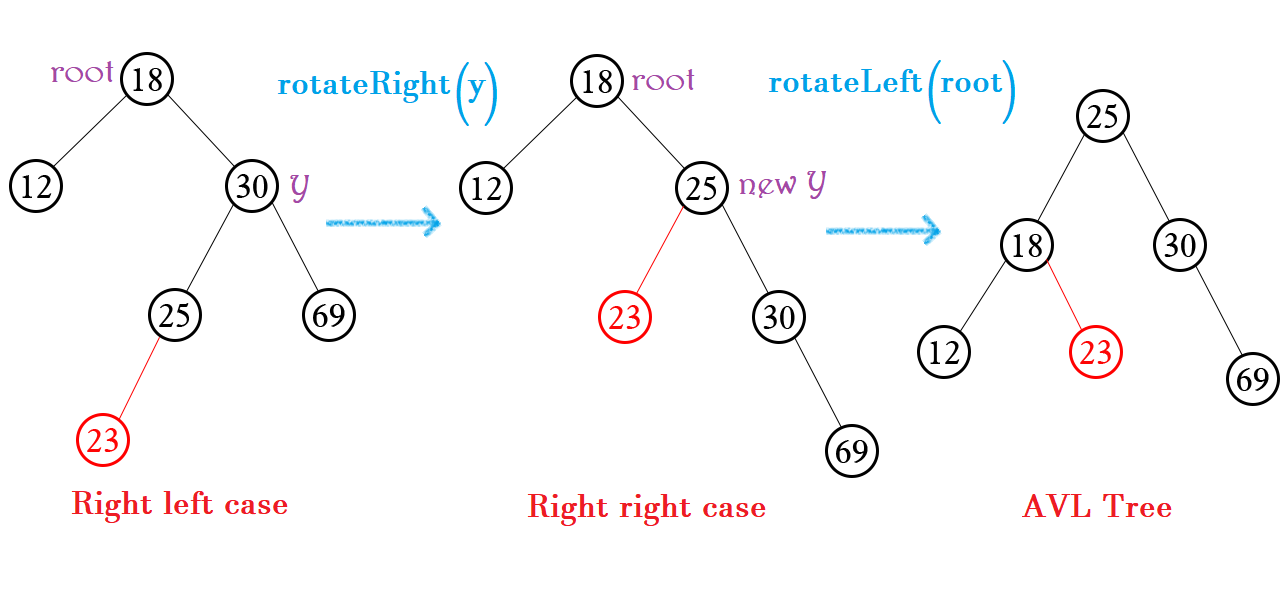
Hoàn toàn tương tự “Trái phải” – Left right
Xảy ra khi: height(X) – height(Y) < -1 và value(Đỏ) < value(Y)
Xử lý: rotateRight(Y) -> rotateLeft(root)
5. Code chính – Insert
#include <iostream>
#include <cmath>
#define COUNT 10
using namespace std;
struct Node {
int data;
Node* left;
Node* right;
int height;
};
int getHeight(Node* root) {
if (root == NULL)
return 0;
//return 1 + max(getHeight(root->left), getHeight(root->right));
return root->height;
}
Node* rightRotate(Node* root){
Node* x = root->left;
// Bắt đầu quay phải
root->left = x->right;
x->right = root;
// Thiết lập chiều cao
root->height = 1 + max(getHeight(root->left), getHeight(root->right));
x->height = 1 + max(getHeight(x->left), getHeight(x->right));
// Return x - trả về root mới
return x;
}
Node* leftRotate(Node* root) {
Node* y = root->right;
// Bắt đầu quay trái
root->right = y->left;
y->left = root;
// Thiết lập chiều cao
root->height = 1 + max(getHeight(root->left), getHeight(root->right));
y->height = 1 + max(getHeight(y->left), getHeight(y->right));
// Return y - trả về root mới
return y;
}
// Insertion - AVL Tree
Node* Insert(Node* root, int value) {
// 1. Insert
if (root == NULL)
return new Node{ value, NULL, NULL, 1 }; // Trả về Node có height = 1
if (value > root->data)
root->right = Insert(root->right, value);
else if (value < root->data)
root->left = Insert(root->left, value);
else
return root; // Neu bang thi khong them
// 2. Set height
root->height = 1 + max(getHeight(root->left), getHeight(root->right));
// 3. Rotate
int valBalance = getHeight(root->left) - getHeight(root->right);
// Kiểm tra 4 TH xảy ra:
// 3.1. Left left
if (valBalance > 1 && value < root->left->data)
return rightRotate(root);
// 3.2. Right Right
if (valBalance < -1 && value > root->right->data)
return leftRotate(root);
// 3.3. Left Right
if (valBalance > 1 && value > root->left->data) {
root->left = leftRotate(root->left);
return rightRotate(root);
}
// 3.4. Right Left
if (valBalance < -1 && value < root->right->data) {
root->right = rightRotate(root->right);
return leftRotate(root);
}
return root;
}
// In - Print 2D ra console
void print2DUtil(Node* root, int space){
if (root == NULL)
return;
space += COUNT;
print2DUtil(root->right, space);
cout << endl;
for (int i = COUNT; i < space; i++)
cout << " ";
cout << root->data << " (" << root->height << ") " << "n";
print2DUtil(root->left, space);
}
void print2D(Node* root){
print2DUtil(root, 0);
}
int main() {
Node* tree = NULL;
tree = Insert(tree, 18);
tree = Insert(tree, 12);
tree = Insert(tree, 30);
tree = Insert(tree, 25);
tree = Insert(tree, 69);
tree = Insert(tree, 23);
print2D(tree);
}Kết quả console
69 (1)
30 (2)
25 (3)
23 (1)
18 (2)
12 (1)
Cảm ơn các bạn đã đọc bài viết của mình. Nếu thấy hay thì hãy chia sẽ nó cho mọi người cùng đọc nhé ! Ngoài ra, bạn nào muốn tham khảo code các ngôn ngữ khác thì hãy truy cập vào Geeks for geeks – AVL Tree.
[sc_quote]Tham khảo các cấu trúc dữ liệu khác trong series Cấu trúc dữ liệu.[/sc_quote]
Thân mến.
Để lại một bình luận