Bài 50. Thuật toán tìm kiếm nhị phân

Thuật toán tìm kiếm nhị phân là một trong các thuật toán sắp xếp được sử dụng rất nhiều trong thực tế. Hãy cùng mình đi tìm hiểu thuật toán tìm kiếm này nhé.

Tìm kiếm là một phần không thể thiếu của mọi ứng dụng, website hay phần mềm. Tính năng tìm kiếm cho phép người sử dụng nhanh chóng truy vấn và tìm kiếm các bản ghi theo mong muốn. Và một công cụ tìm kiếm nổi tiếng nhất hàng ngày chúng ta vẫn thường sử dụng đó là Google search.

Bài viết ngày hôm nay Nguyễn Văn Hiếu sẽ giới thiệu cho độc giả một thuật toán tìm kiếm tối ưu áp dụng đối với trường hợp dữ liệu số đã sắp xếp.

Đối với các giải thuật sắp xếp, các bạn có thể đọc thêm tại: series các thuật toán sắp xếp

Phát biểu thuật toán tìm kiếm nhị phân(Binary search)

Cho một mảng đã sắp xếp arr[] có n phần tử, viết một hàm tìm kiếm trả về chỉ số của phần tử có giá trị x trong arr[].

Giải thuật đơn giản nhất cho bài toán này là sử dụng linear search(tìm kiếm tuyến tính). Tức là bạn sẽ phải đi qua từng phần tử của mảng để đối chiếu với x cần tìm. Thuật toán này trong trường hợp xấu nhất cho độ phức tạp là O(n). Mình cũng sẽ minh họa code của thuật toán này dưới đây.

Đây là code C/C++ sử dụng linear search.

// Code from https://nguyenvanhieu.vn

#include <stdio.h>

int search(int arr[], int n, int x)
{
  int i;
  for (i = 0; i < n; i++)
    if (arr[i] == x)
      // Trả về chỉ số khi tìm thấy
      return i;
  // Nếu không tìm thấy trả về -1. Vì chỉ số mảng >= 0
  return -1;
}

int main() {
  int arr[] = {2, 3, 4, 10, 40};
  int n = sizeof(arr) / sizeof(arr[0]);
  int x = 10;
  int result = search(arr, n, x);
  if (result != -1) {
    printf("%d xuat hien tai chi so %d", x, result);
  } else {
    printf("%d khong co trong mang", x);
  }
  return 0;
}

Ý tưởng của thuật toán tìm kiếm nhị phân

Chú ý: Trong bài viết tôi giả sử mảng đang sắp xếp tăng dần. Với trường hợp mảng sắp xếp giảm dần, bạn đọc sau khi hiểu thuật toán sẽ có thể tự làm.

Do tính chất mảng đã sắp xếp, công việc tìm kiếm phần tử x có thể triển khai như sau:

1. Xét đoạn mảng arr[left…right] cần tìm kiếm phần tử x. Ta so sánh x với phần tử ở vị trí giữa của mảng(mid = (left + right)/2). Nếu:
2. Nếu phần tử arr[mid] = x. Kết luận và thoát chương trình.
3. Nếu arr[mid] < x. Chỉ thực hiện tìm kiếm trên đoạn arr[mid+1…right].
4. Nếu arr[mid] > x. Chỉ thực hiện tìm kiếm trên đoạn arr[left…mid-1].

Hình ảnh dưới đây mô phỏng quá trình thực hiện của thuật toán tìm kiếm nhị phân và so sánh với thuật toán tìm kiếm tuyến tính.

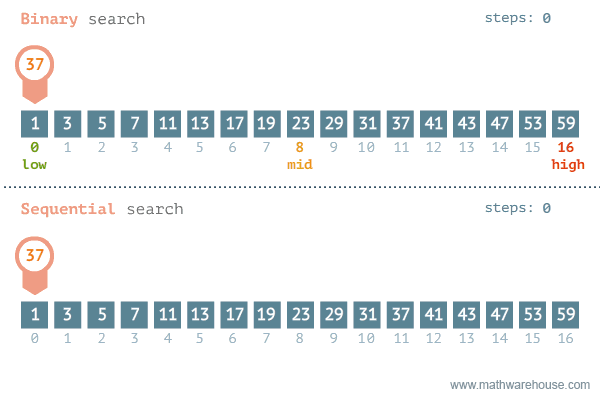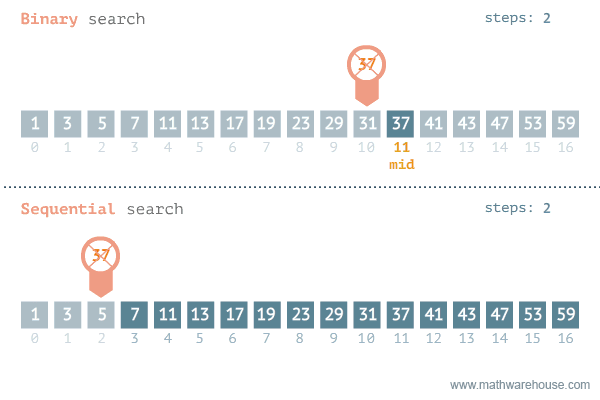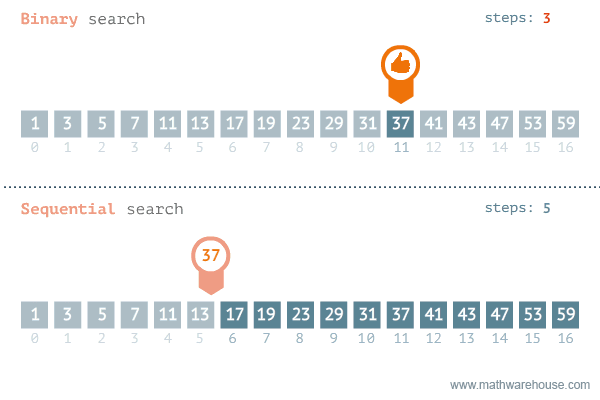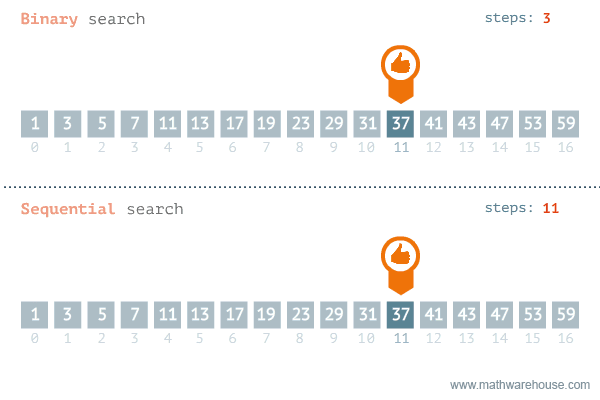
Bằng cách áp dụng thuật toán tìm kiếm nhị phân, độ phức tạp cho trường hợp xấu nhất là O(log(n)).

Dành cho bạn: Sau bài học này, bạn có thể áp dụng kiến thức tìm kiếm nhị phân vào thực hành các bài tập tại Luyện Code.

Minh họa code cho thuật toán tìm kiếm nhị phân

Trong phần này, mình sẽ minh họa code sử dụng giải thuật đệ quy dùng Java và C/C++. Ngoài ra, tôi sẽ áp dụng thêm giải thuật khử đệ quy với C/C++.

Code minh họa C/C++ sử dụng đệ quy

// Code from https://nguyenvanhieu.vn

#include <stdio.h>

// Hàm tìm kiếm nhị phân sử dụng giải thuật đệ quy
int binarySearch(int arr[], int l, int r, int x) {
  if (r >= l) {
    int mid = l + (r - l) / 2; // Tương đương (l+r)/2 nhưng ưu điểm tránh tràn số khi l,r lớn

    // Nếu arr[mid] = x, trả về chỉ số và kết thúc.
    if (arr[mid] == x)
      return mid;

    // Nếu arr[mid] > x, thực hiện tìm kiếm nửa trái của mảng
    if (arr[mid] > x)
      return binarySearch(arr, l, mid - 1, x);

    // Nếu arr[mid] < x, thực hiện tìm kiếm nửa phải của mảng
    return binarySearch(arr, mid + 1, r, x);
  }

  // Nếu không tìm thấy
  return -1;
}

int main(void) {
  int arr[] = {2, 3, 4, 10, 40};
  int n = sizeof(arr) / sizeof(arr[0]);
  int x = 10;
  int result = binarySearch(arr, 0, n - 1, x);
  if (result == -1)
    printf("%d xuat hien tai chi so %d", x, result);
  else
    printf("%d xuat hien tai chi so %d", x, result);
  return 0;
}

Code minh họa sử dụng đệ quy Java

// Code from https://nguyenvanhieu.vn

class BinarySearch {
  
  int binarySearch(int arr[], int l, int r, int x) {
    if (r >= l) {
      int mid = l + (r - l) / 2;

      // Nếu arr[mid] = x, trả về chỉ số và kết thúc
      if (arr[mid] == x)
        return mid;

      // Nếu arr[mid] > x, gọi đệ quy tìm kiếm bên trái
      if (arr[mid] > x)
        return binarySearch(arr, l, mid - 1, x);

      // Ngược lại, nếu arr[mid] < x, gọi đệ quy tìm kiếm bên phải
      return binarySearch(arr, mid + 1, r, x);
    }

    // Trong trường hợp không tìm thấy
    return -1;
  }

 
  public static void main(String args[]) {
    BinarySearch ob = new BinarySearch();
    int arr[] = {2, 3, 4, 10, 40};
    int n = arr.length;
    int x = 10;
    int result = ob.binarySearch(arr, 0, n - 1, x);
    if (result == -1)
      System.out.println("Không tìm thấy phần tử " + x);
    else
      System.out.println("Phần tử " + x + " được tìm thấy tại chỉ số " +
                         result);
  }
}

Code khử đệ quy sử dụng C/C++

// Code from https://nguyenvanhieu.vn

#include <stdio.h>

// Hàm tìm kiếm nhị phân sử dụng giải thuật đệ quy
int binarySearch(int arr[], int n, int x) {
  int r = n - 1; // chỉ số phần tử cuối
  int l = 0; // Chỉ số phần tử đầu tiên
  while (r >= l) {
    int mid = l + (r - l) / 2; // Tương đương (l+r)/2 nhưng ưu điểm tránh tràn số khi l,r lớn

    // Nếu arr[mid] = x, trả về chỉ số và kết thúc.
    if (arr[mid] == x)
      return mid;

    // Nếu arr[mid] > x, cập nhật lại right
    if (arr[mid] > x)
      r = mid - 1;
    // Nếu arr[mid] < x, cập nhật lại left
    if (arr[mid] < x)
      l = mid + 1;
  }

  // Nếu không tìm thấy
  return -1;
}

int main(void) {
  int arr[] = {
    2,
    3,
    4,
    10,
    40
  };
  int n = sizeof(arr) / sizeof(arr[0]);
  int x = 10;
  int result = binarySearch(arr, n, x);
  if (result == -1)
    printf("%d xuat hien tai chi so %d", x, result);
  else
    printf("%d xuat hien tai chi so %d", x, result);
  return 0;
}