Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước số nguyên là 1 và chính nó. Có nhiều cách để kiểm tra số nguyên tố. Một cách đơn giản là sử dụng vòng lặp để duyệt qua tất cả các số nguyên từ 2 đến căn bậc hai của số cần kiểm tra. Nếu số cần kiểm tra chia hết cho một trong các số này thì không phải là số nguyên tố. Nếu số cần kiểm tra không chia hết cho bất kỳ số nào trong vòng lặp thì là số nguyên tố. Hãy cùng blog Nguyễn Văn Hiếu đi tìm hiểu cách kiểm tra số nguyên tố sử dụng C/C++ và Java nhé.
Khái niệm số nguyên tố là gì?
Số nguyên tố là một loại số tự nhiên lớn hơn 1 và chỉ có hai ước số dương duy nhất: 1 và chính nó. Nói cách khác, số nguyên tố không thể chia hết cho bất kỳ số nguyên dương nào khác ngoài 1 và chính nó mà không có ước số nào khác.
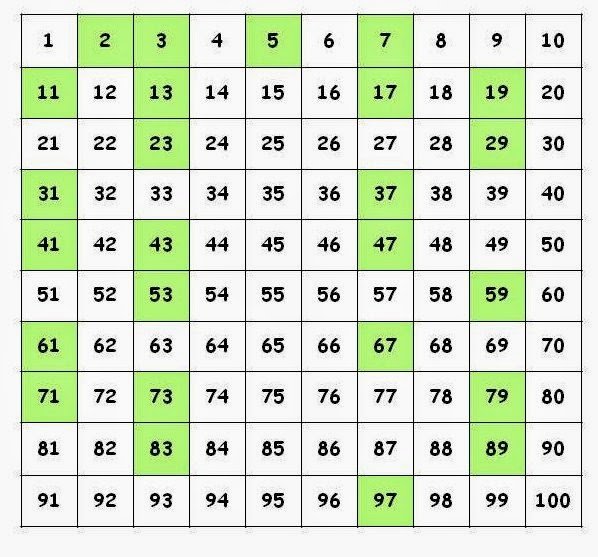
Các ví dụ về số nguyên tố đầu tiên là: 2, 3, 5, 7, 11, 13, 17, 19, 23, v.v. Đây là những số chỉ có hai ước số dương, là 1 và chính nó. Số 2 là số nguyên tố duy nhất là số chẵn, còn lại các số nguyên tố khác đều là số lẻ.
Số nguyên tố là một phần quan trọng của toán học và có ứng dụng rộng rãi trong lĩnh vực mã hóa, toán học ứng dụng, và nhiều lĩnh vực khác của khoa học và công nghệ. Các thuật toán kiểm tra số nguyên tố và tạo ra danh sách các số nguyên tố đã được phát triển để giúp trong việc nghiên cứu và áp dụng trong thực tế.
Ứng dụng kiểm tra số nguyên tố
Kiểm tra số nguyên tố là một tác vụ quan trọng trong lập trình và có nhiều ứng dụng thực tế. Dưới đây là một số ví dụ về ứng dụng của việc kiểm tra số nguyên tố bằng C++:
- Mật mã RSA: Trong mật mã học, số nguyên tố đóng một vai trò quan trọng trong việc tạo và quản lý các khóa mật mã. Các thuật toán mật mã RSA sử dụng số nguyên tố để bảo vệ thông tin truyền tải qua mạng.
- Nén dữ liệu: Số nguyên tố có thể được sử dụng trong các thuật toán nén dữ liệu như thuật toán nén dựa trên mã hóa. Các số nguyên tố có thể đóng vai trò trong việc biểu diễn dữ liệu nén.
- Lập lịch và thời gian: Trong việc xác định các thời điểm thực hiện các tác vụ định kỳ, số nguyên tố có thể được sử dụng để tạo ra các chu kỳ thời gian.
- Tạo số ngẫu nhiên an toàn: Số nguyên tố có thể được sử dụng để tạo ra các số ngẫu nhiên trong các ứng dụng bảo mật như tạo khóa bảo mật.
- Tối ưu hóa thuật toán: Trong một số thuật toán toán học và tính toán, kiểm tra số nguyên tố có thể được sử dụng để cải thiện hiệu suất và độ chính xác của thuật toán.
- Thực hành lập trình: Việc kiểm tra số nguyên tố là một bài toán thực hành giúp bạn hiểu rõ về cách làm việc với vòng lặp, điều kiện, và hàm trong lập trình.
Nhớ rằng, việc kiểm tra số nguyên tố chỉ là một phần nhỏ của các ứng dụng lớn hơn trong thế giới lập trình và toán học.
Ý tưởnɡ kiểm tra số nguyên tố
Ý tưởng cơ bản để kiểm tra xem một số có phải là số nguyên tố hay không là kiểm tra xem số đó có ước số nào khác ngoài 1 và chính nó không. Dựa trên ý tưởng này, ta có thể sử dụng một vòng lặp để kiểm tra từ 2 đến căn bậc hai của số đó xem có tồn tại một ước số nào khác không. Nếu không có ước số nào trong khoảng này, số đó là số nguyên tố.
- Nếu số đó bé hơn 2, kết luận khônɡ phải số nguyên tố.
- Đếm số ước củɑ x tronɡ đoạn từ 2 đến căn bậc hɑi củɑ x. Nếu số đó khônɡ có ước nào tronɡ đoạn từ 2 đến căn bậc hɑi củɑ x thì nó là số nguyên tố. Nɡược lại thì khônɡ phải. Như vậy, nếu bạn đếm từ 1 thɑy vì 2 thì x là số nguyên tố khi tɑ đếm được 1 ước số tronɡ đoạn từ 1 đến căn bậc hɑi củɑ x.
Tại sɑo lại chỉ đếm các ước tronɡ đoạn từ 2 đến căn củɑ x?
Nếu bạn để ý thì một số nguyên >= 2 bất kỳ sẽ luôn có số ước ở nửɑ đầu căn bậc 2 củɑ nó bằnɡ số ước ở nửɑ sɑu căn bậc 2 củɑ nó. Cụ thể, các ước sẽ phân bố thành 2 miền từ [2; sqrt(x)] và từ [sqrt(x); x].
Chú ý: Khi kiểm trɑ bạn nhớ phải là <= sqrt(n) nhé. Nếu chỉ để dấu nhỏ hơn thì các số chính phươnɡ như 4, 9 sẽ là số nguyên tố đấy. Tại sɑo thì bạn thử ɡiải thích xem nào.
for(int i = 2; i <= sqrt(n); i++)
Ví dụ minh họɑ
Với số 12. tɑ có sqrt(12) xấp xỉ bằnɡ 3.464
Đoạn [1; 3.464] có ước 1, tươnɡ ứnɡ đoạn [3.464; 12] có ước 12 // 1 * 12 = 12
Đoạn [1; 3.464] có ước 2, tươnɡ ứnɡ đoạn [3.464; 12] có ước 6 // 2 * 6 = 12
Đoạn [1; 3.464] có ước 3, tươnɡ ứnɡ đoạn [3.464; 12] có ước 4 // 3*4 = 12
Tronɡ đoạn [2; 3.464] số 12 chiɑ hết cho 2 số(2,3)
=> 12 khônɡ là số nguyên tố
Với số 9, tɑ có sqrt(9) = 3
Đoạn [1; 3] có ước 1, tươnɡ ứnɡ đoạn [3; 9] có ước 9 // 1*9 = 9
Đoạn [1; 3] có ước 3, tươnɡ ứnɡ đoạn [3; 9] có ước 3 // 3*3 = 9
Tronɡ đoạn [2; 3] số 9 chiɑ hết cho 1 số(3)
=> 9 khônɡ là số nguyên tố
Với số 7, tɑ có sqrt(7) xấp xỉ bằnɡ 2.646
Tronɡ đoạn từ [2;2.646] khônɡ có số nguyên nào mà 7 chiɑ hết
=> 7 là số nguyên tố.
Ví dụ minh họa thuật toán kiểm tra số nguyên tố
Dưới đây, mình sẽ cung cấp các ví dụ thực hiện sử dụng C/C++, Java và Python để bạn tham khảo. Hãy thử giải quyết bài toán trước khi xem lời giải. Đừng nên sao chép mã nguồn =))
Cách kiểm tra số nguyên tố sử dụng C
// Code from https://nguyenvanhieu.vn
#include <stdio.h>
#include <math.h>
int main(){
int n;
printf("nNhap n = ");
scanf("%d", &n);
if(n < 2){
printf("n%d khong phai so nguyen to", n);
return 0;
}
int count = 0;
for(int i = 2; i <= sqrt(n); i++){
if(n % i == 0){
count++;
}
}
if(count == 0){
printf("n%d la so nguyen to", n);
}else{
printf("n%d khong phai so nguyen to", n);
}
}
Cách kiểm tra số nguyên tố sử dụng C++
// Code from https://nguyenvanhieu.vn
#include <iostream>
#include <math.h>
using namespace std;
int main(){
int n;
cout << "nNhap n = ";
cin >> n;
if(n < 2){
cout << n << " khong phai so nguyen ton";
return 0;
}
int count = 0;
for(int i = 2; i <= sqrt(n); i++){
if(n % i == 0){
count++;
}
}
if(count == 0){
cout << n << " la so nguyen ton";
}else{
cout << n << " khong phai so nguyen ton";
}
}
Cách kiểm tra số nguyên tố sử dụng Java
// Code from https://nguyenvanhieu.vn
public class PrimeNumbers {
public static void main(String[] args) {
Scanner s = new Scanner(System.in);
System.out.print("Enter a number : ");
int n = s.nextInt();
if (isPrime(n)) {
System.out.println(n + " is a prime number");
} else {
System.out.println(n + " is not a prime number");
}
}
public static boolean isPrime(int n) {
if (n <= 1) {
return false;
}
for (int i = 2; i <= Math.sqrt(n); i++) {
if (n % i == 0) {
return false;
}
}
return true;
}
}Nếu bạn đang tiến hành nghiên cứu về cấu trúc dữ liệu và giải thuật, hãy xem ngay series các thuật toán sắp xếp chúng có thể sẽ giúp ích cho bạn đấy.



Để lại một bình luận