Viết chương trình tính e mũ x

Bài toán: Viết chương trình có dùng hàm để tính e mũ x theo công thức sau:

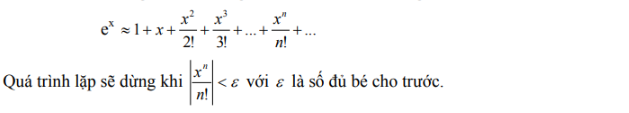
Hướng dẫn giải quyết bài toán

Nhìn trên dãy khai triển trên ta có thể thấy chúng có cùng một công thức chính là 

Vậy chúng ta sẽ viết một hàm tính lũy thừa và một hàm tính giai thừa là gần như đã giải quyết được bài toán trên.

Xây dựng hàm tính giai thừa

Code tham khảo:

float giaiThua(int n) {
	int giaithua = 1;
	for (int i = 1; i <= n; i++)
		giaithua *= i;
	return (float) giaithua;
}

Xây dựng hàm tính lũy thừa

Code tham khảo:

float luyThua(int n, int k) {
	int pow = 1;
	for (int i = 1; i <= k; i++)
		pow *= n;
	return (float) pow;
}

Giải quyết bài toán tính e mũ x

Xây dựng hàm tính e mũ x theo dãy khai triển

Ở phía trên chúng ta đã viết hai hàm đó là hàm tính giai thừa và hàm tính lũy thừa rồi phải không nào !

Bây giờ nhiệm vụ còn lại là tính e mũ x theo dãy khai triển trên mà thôi. Ta sẽ sử dụng một vòng lặp while để tính e mũ x như sau:

• Khởi tạo một giá trị sum bằng 0.
• Nếu xⁿ / n! > ε thì ta cộng giá trị sum cho xⁿ / n!
• Quá trình sẽ lặp đi lặp lại đến khi điều kiện trên sai( tức là sai số không quá lớn).
• Ta sẽ cho số ε rất nhỏ cỡ 0.0000001 để quá trình tính toán chính xác hơn.

Code tính e mũ x:

#include <stdio.h>

float luyThua(int n, int k) {
	int pow = 1;
	for (int i = 1; i <= k; i++)
		pow *= n;
	return (float)pow;
}

float giaiThua(int n) {
	int giaithua = 1;
	for (int i = 1; i <= n; i++)
		giaithua *= i;
	return (float)giaithua;
}

float fun(int x) {
	float sum = 0;
	int i = 0;
	while (luyThua(x, i) / giaiThua(i) > 1e-10 ) {
		sum += luyThua(x, i) / giaiThua(i);
		i++;
	}
	return sum;
}

int main() {
	int x;
	printf("Nhap x: ");
	scanf("%d", &x);
	printf("e^x: %6f", fun(x));
	return 0;
}

Nhap x: 1
e^x: 2.718282

Các bạn chú ý là hai hàm tính lũy thừa và giai thừa của mình đã được ép kiểu về float hết rồi nhé. Nếu các bạn không ép kiểu thì kết quả sẽ bị sai đấy !

Tối ưu chương trình hơn

Nếu bạn nào để ý thì sẽ nhận ra điều sau: 

Vậy nên chúng ta sẽ chỉ cần dùng một vòng while để tính e mũ x mà thôi. Không cần phải viết hai hàm tính lũy thừa và giai thừa như trên nữa. Hơn nữa với số mũ lớn thì cách này tỏ ra vượt trội hoàn toàn so với cách ở trên. Độ chính xác cũng cao hơn các trên, vậy thì tại sao lại không dùng nào ?

Ban đầu mình sẽ khởi tạo một biến sum = 1, i = 1 và một biến temp = x . Sau đó kiểm tra nếu temp > ε thì ta tiến hành cộng thêm vào giá trị temp cho sum. Sau đó ta nhân temp với x / i và tiến hành tăng giá trị i lên một đơn vị. Qúa trình cứ lặp đi lặp lại cho đến khi điều kiện trong vòng while bị sai.

Code tham khảo:

#include <stdio.h>

float fun(int x) {
	float sum = 1;
	int i = 1;
	float temp = x;
	while ( temp > 1e-10 ) {
		sum += temp;
		i++;
		temp = temp * x / i;
	}
	return sum;
}

int main() {
	int x;
	printf("Nhap x: ");
	scanf("%d", &x);
	printf("e^x: %6f", fun(x));
	return 0;
}

Nhap x: 10
e^x: 22026.468750

Với số mũ lớn như 10 thì độ chính xác vẫn rất cao !

Bài viết mình đến đây là kết thúc. Cám ơn các bạn đã theo dõi !