Bài viết hôm nay mình sẽ hướng dẫn các bạn cách giải bài toán mã đi tuần. Nào chúng ta cùng bắt đầu thôi !
Giới thiệu bài toán mã đi tuần
Bài toán mã đi tuần
Mã đi tuần (hay hành trình của quân mã) là bài toán về việc di chuyển một quân mã trên bàn cờ vua (8 x 8). Quân mã được đặt ở một ô trên một bàn cờ trống nó phải di chuyển theo quy tắc của cờ vua để đi qua mỗi ô trên bàn cờ đúng một lần.
Nếu một quân mã đi hết 64 vị trí và tại vị trí cuối cùng có thể di chuyển đến vị trí bắt đầu thông qua một nước cờ thì đó gọi là một hành trình đóng
Có những hành trình, trong đó quân mã sau khi đi hết tất cả 64 ô của bàn cờ và từ ô cuối của hành trình không thể đi về ô xuất phát chỉ bằng một nước đi. Những hành trình như vậy được gọi là hành trình mở.
Ví dụ sau đây là một lời giải cho bài toán mã đi tuần trên bàn cờ 5×5 (hành trình mở).

Cách di chuyển của một quân mã
Nước đi của một quân mã giống hình chữ L và nó có thể di chuyển tất cả các hướng. Ở một vị trí thích hợp thì quân mã có thể di chuyển đến được 8 vị trí.
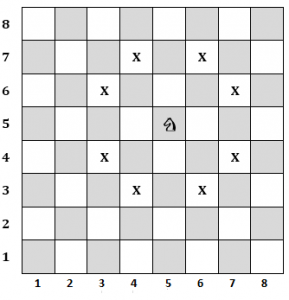
Hướng dẫn giải bài toán mã đi tuần
Xây dựng bước đi cho quân mã
Giọi x,y là độ dài bước đi trên các trục Oxy. Một bước đi hợp lệ của quân mã sẽ như sau: |x| + |y| = 3 ( Với x,y > 0).
Khi đó ở một vị trí bất kì quân mã có có 8 đường có thể di chuyển. Chưa xét đến bước đi đó có hợp lệ hay không.
Các bước đi đó là: ( -2, -1), ( -2, 1), ( -1, -2), ( -1, 2), ( 1, -2), ( 1, 2), ( 2, -1), ( 2, 1)
Để đơn giản ta sẽ tạo hay mảng X[], Y[] để chứa các giá trị trên. Với mỗi X[i], Y[i] sẽ là một cách di chuyển của quân mã(0 ≤i≤ 7 ).
Kiểm tra tính hợp lệ của bước đi
Ta sẽ dùng một mảng hai chiều A[n*n] để lưu vị trí của từng ô trong bàn cờ. Tất cả mảng đều khởi tạo giá trị là 0( quân mã chưa đi qua).
Giọi x,y là vị trí hiện tại của quân mã, thì vị trí tiếp theo mà quân mã đi sẽ có dạng x+X[i], y+Y[i]. Một vị trí được gọi là hợp lệ thì sẽ thỏa mãn tính chất sau:
- 0 ≤ x+X[i]≤ n-1.
- 0 ≤ x+X[i]≤ n-1.
Nếu bước đi đó là bước đi đúng thì ta sẽ lưu thứ tự của bước đi đó vào mảng A[ x+X[i], y+Y[i] ].
Giải bài toán mã đi tuần bằng đệ quy
Khởi tạo các giá trị ban đầu
#include<iostream>
#define MAX 8
using namespace std;
int A[MAX][MAX] = { 0 };//Khởi tạo mảng giá trị 0
int X[8] = { -2,-2,-1,-1, 1, 1, 2, 2};
int Y[8] = { -1, 1,-2, 2,-2, 2,-1, 1};
int n;// Số phần tử của bàn cờ bạn muốn tạo
int main() {
}
Xây dựng hàm xuất mảng
void xuat() {
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
cout << A[i][j] << " ";
cout << endl;
}Xây dựng hàm bước đi
void diChuyen(int x, int y) {
++dem;//Tăng giá trị bước đi
A[x][y] = dem;//Đánh dấu đã đi
//Tìm tất cả các bước đi có thể đi và tiến hành đi thử
for (int i = 0; i < 8; i++) {
//Kiểm tra xem mã đã đi hết bàn cờ chưa
if (dem == n * n) {
cout << "Cac buoc di la: n";
xuat();
exit(0);//kết thúc chương trình
}
//Nếu chưa đi hết bàn cờ thì tạo bước đi mới
int u = x + X[i];//tạo một vị trí x mới
int v = y + Y[i];//tạo một vịi trí y mới
//Nếu hợp lẹ thì tiến hành di chuyển
if (u >= 0 && u < n&&v >= 0 && v < n&& A[u][v] == 0)
diChuyen(u, v);
}
//Nếu không tìm được bước đi thì ta phải trả lại các giá trị ban đầu
--dem;
A[x][y] = 0;
}Có lẽ hàm diChuyen() chính là hàm quan trọng nhất vì nó quyết định cách di chuyển của một quân mã. Ý tưởng của hàm là từ một vị trí ban đầu ta sẽ tìm một bước di chuyển hợp lệ và di chuyển đến vị trí đó. Tiếp tục tìm một bước đi và di chuyển tiếp đến khi không thể di chuyển được nữa (vào thế bí ) thì sẽ xóa bước đi đó. Chương trình chỉ dừng khi tìm được một hành trình hoặc đã thử di chuyển hết tất cả các bước đi nhưng vẫn không tìm thấy hành trình.
#include<iostream>
#include<stdio.h>
#define MAX 8
using namespace std;
int A[MAX][MAX] = { 0 };//Khởi tạo mảng giá trị 0
int X[8] = { -2,-2,-1,-1, 1, 1, 2, 2};
int Y[8] = { -1, 1,-2, 2,-2, 2,-1, 1};
int dem = 0;//Số bước đi
int n;
void xuat() {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++)
printf("%2d ", A[i][j]);
cout << endl;
}
cout << endl;
}
void diChuyen(int x, int y) {
++dem;//Tăng giá trị bước đi
A[x][y] = dem;//Đánh dấu đã đi
for (int i = 0; i < 8; i++) {
//Kiểm tra xem mã đã đi hết bàn cờ chưa
if (dem == n * n) {
cout << "Cac buoc di la: n";
xuat();
exit(0);//kết thúc chương trình
}
//Nếu chưa đi hết bàn cờ thì tạo bước đi mới
int u = x + X[i];//tạo một vị trí x mới
int v = y + Y[i];//tạo một vịi trí y mới
//Nếu hợp lẹ thì tiến hành di chuyển
if (u >= 0 && u < n&&v >= 0 && v < n&& A[u][v] == 0)
diChuyen(u, v);
}
//Nếu không tìm được bước đi thì ta phải trả lại các giá trị ban đầu
--dem;
A[x][y] = 0;
}
int main() {
cout << "Nhap n: ";
cin >> n;
int a, b;
cout << "Nhap vi tri ban dau.nx: ";
cin>>a;
cout << "y: ";
cin >> b;
diChuyen(a, b);
//Nếu không tìm được bước đi thì sẽ thông báo
cout << "Khong tim thay duong di.";
}Nhap n: 5 Nhap vi tri ban dau. x: 0 y: 0 Cac buoc di la: 1 18 5 10 3 6 11 2 19 14 17 22 13 4 9 12 7 24 15 20 23 16 21 8 25
Nếu bạn muốn tìm một chu trình đóng thì các bạn cần lưu lại vị trí ban đầu. Ví dụ x_first, y_first sau đó kiểm tra như sau:
if (dem == n * n && x==x_first && y==y_first) {
cout << "Cac buoc di la: n";
xuat();
exit(0);//kết thúc chương trình
}Bài viết của mình đến đây là kết thúc. Cám ơn các bạn đã theo dõi !



Để lại một bình luận