Bài toán Tháp Hà Nội là một trò chơi toán học cổ điển được đặt theo tên của thành phố Hà Nội, Việt Nam. Bài toán bao gồm ba cọc và một số đĩa có kích thước khác nhau, được xếp chồng lên nhau trong cọc đầu tiên, nhỏ nhất ở trên cùng. Mục tiêu của bài toán là di chuyển toàn bộ đĩa sang cọc thứ ba, tuân theo các quy tắc sau:
- Mỗi lần chỉ được di chuyển một đĩa.
- Không có đĩa nào có thể được đặt trên một đĩa nhỏ hơn.
- Được phép sử dụng cọc thứ hai làm cọc trung gian để di chuyển các đĩa.
Bài toán tháp Hà Nội (Tower of Ha Noi )
Trước khi tìm hiểu cách giải bài toán tháp Hà Nội (Tower of Hanoi), mình xin nhắc lại các quy tắc của trò chơi Tháp Hà Nội này:
Bài toán tháp Hà Nội ( Tower of Hà Nội ) là một trò chơi toán học gồm 3 cột và số đĩa nhiều hơn 1. Trong hình dưới mô tả trò chơi gồm có ba đĩa
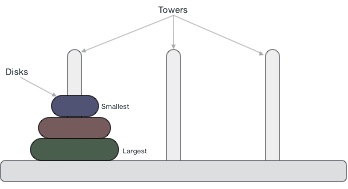
Với quy tắc các đĩa nhỏ phải nằm trên các đĩa lớn. Với số đĩa khác nhau thì ta có các bài toán Tháp Hà Nội khác nhau, tuy nhiên cách giải là vẫn vậy.
Qui tắc trò chơi toán học Tháp Hà Nội (Tower of Hanoi)
Nhiệm vụ của trò chơi là di chuyển các đĩa có kích cỡ khác nhau sang cột khác sao cho vẫn đảm bảo thứ tự ban đầu của các đĩa: đĩa nhỏ nằm trên đĩa lớn. Dưới đây là một số qui tắc cho trò chơi toán học Tháp Hà Nội (Tower of Hanoi):
Hình ảnh dưới đây là mô tả cách giải bài toán tháp Hà Nội
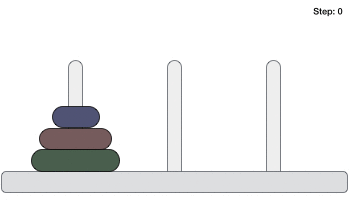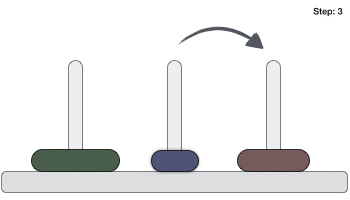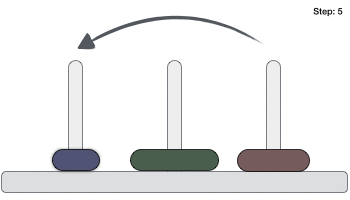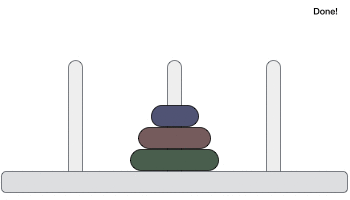
Mục đích của bài toán là thực hiện được yêu cầu của trò chơi. Dạng bài toán thông dụng nhất là: “Người chơi được cho ba cái cọc và một số đĩa có kích thước khác nhau có thể cho vào các cọc này. Ban đầu sắp xếp các đĩa theo trật tự kích thước vào một cọc sao cho đĩa nhỏ nhất nằm trên cùng. Người chơi phải di chuyển toàn bộ số đĩa sang một cọc khác, tuân theo các quy tắc sau:
- một lần chỉ được di chuyển một đĩa
- một đĩa chỉ có thể được đặt lên một đĩa lớn hơn
Bài toán tháp Hà Nội với n đĩa thì có ít nhất 2^n – 1 bước thực hiện. Với ví dụ trên là 3 đĩa thì số bước giải ít nhất là 2^3-1=7 cách giải.
Cách giải bài toán tháp Hà Nội bằng đệ quy
Qui ước: Đặt tên 3 cột là A B C để tiện theo dõi. Yêu cầu bài toán là chuyển n chiếc đĩa từ cột A sang cột C
Cách giải
- Đầu tiên ta lấy cột C làm cọc trung gian. Chuyển n-1 chiếc đĩa sang cột B.
- Ta chuyển chiếc đĩa lớn nhất sang cột C
- Lấy cột A làm cột trung gian chuyển n-1 chiếc đĩa từ cột B sang cột C
Hình ảnh dưới đây miêu tả cách giải này

Code C++
#include<iostream>
using namespace std;
void Tower(int n , char a, char b, char c ){
if(n==1){
cout<<"t"<<a<<"-------"<<c<<endl;
return;
}
Tower(n-1,a,c,b);
Tower(1,a,b,c);
Tower(n-1,b,a,c);
}
int main(){
char a='A', b='B', c='C';
int n;
cout<<"Nhap n: ";
cin>>n;
Tower(n,a,b,c);
}Nhap n: 3
A-------C
A-------B
C-------B
A-------C
B-------A
B-------C
A-------C
Code C
#include<stdio.h>
void Tower(int n , char a, char b, char c ){
if(n==1){
printf("t%c-------%cn",a,c);
return;
}
Tower(n-1,a,c,b);
Tower(1,a,b,c);
Tower(n-1,b,a,c);
}
int main(){
char a='A', b='B', c='C';
int n;
printf("Nhap n: ");
scanf("%d",&n);
Tower(n,a,b,c);
}Nhap n: 3
A-------C
A-------B
C-------B
A-------C
B-------A
B-------C
A-------CBài viết của mình đến đây là kết thúc. Cám ơn các bạn đã theo dõi !



Để lại một bình luận