Đệ quy (recursion) là một phần khá trừu tượng và cũng tương đối là khó hiểu đối với những bạn mới tiếp xúc với lập trình. Nên trong bài viết này hôm nay mình sẽ cố gắng trình bày một cách dễ hiểu nhất cho cả những bạn đã nắm bắt sơ sơ về lập trình cũng như là những bạn mới tiếp xúc nhé !
Đệ quy trong C# là gì ?
Theo Wikipedia, trong khoa học máy tính, đệ quy thường được hiểu là một cấu trúc, phương thức mà trong đó các thao tác xử lý bên trong sẽ gọi lại hoặc thực thi lại chính nó. Đệ quy hay được sử dụng bởi các lập trình viên khi thao tác với một dãy có quy luật và công thức truy hồi mang tính truy ngược lại các giá trị ở vị trí trước như dãy số Fibonacci, Giai thừa …
Đó là cách hiểu đơn giản nhất, nhưng về bản chất “Một đối tượng được coi là đệ quy nếu nó được định nghĩa qua chính nó hoặc một đối tượng khác cùng dạng với chính nó bằng quy nạp”.
Nhìn các định nghĩa có vẻ hơi khó hiểu đúng không ? Để dễ hiểu hơn, mình sẽ trình bày các ví dụ sử dụng đệ quy trong phần sau đây.
Các ví dụ với đệ quy
Tính số Fibonacci thứ N
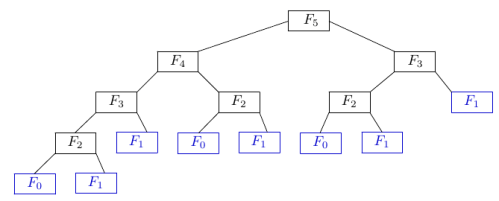
Đệ quy thường được mô tả rõ nhất khi sử dụng để tính một số trong dãy số Fibonacci (dãy Fibo).
Với dãy số được ký hiệu là [latex]F[/latex] chúng ta có công thức truy hồi như sau:
[latex]F_0 = 0, F_1 = 1, F_2 = 1, F_{n} = F_{n-1} + F_{n-2}[/latex]
Chúng ta thấy [latex]F_n[/latex] sẽ bằng tổng 2 số trước nó vì vậy, chúng ta sử dụng đệ quy để làm bài toán này như sau. Ở đây mình sẽ không viết cả chương trình mà thay vào đó mình chỉ viết đoạn code của hàm đệ quy tính số Fibonacci thứ [latex]n[/latex].
int fibo(int n) {
if (n == 1 || n == 2)
return 1;
if (n == 0)
return 0;
return fibo(n - 1) + fibo(n - 2);
}Giải thích một chút về đoạn code trên, mình đã viết một hàm fibo phục vụ cho việc tính số Fibonacci thứ N, mà [latex]F_{n} = F_{n-1} + F_{n-2}[/latex] nên mỗi giá trị trả về chúng ta tính giá trị của fibo(n - 1) + fibo(n - 2). Ngoài ra trong đoạn code này mình đã để thêm 2 câu lệnh logic, vì trong dãy số Fibonacci định nghĩa rằng [latex]F_0 = 0, F_1 = 1, F_2 = 1[/latex] cũng là 3 số được định nghĩa duy nhất trong dãy số, nên mình đã sử dụng các câu lệnh logic này trong việc trả về số tại các vị trí 0, 1 và 2. Nếu không có những điều kiện này, chương trình đệ quy của chúng ta sẽ chạy vô hạn và dẫn tới việc bị tràn bộ nhớ.
Lưu ý: Điều kiện để một hàm đệ quy dừng lại con được gọi là “Phần neo”.
Các bạn có thể chạy thử với hàm trên, giả sử tính số thứ 11 trong dãy Fibonacci thì các bạn hãy gọi fibo(11). Và thử so sánh với dãy số Fibonacci chuẩn xem kết quả trả ra có đúng hay không nhé !
Tính n! (giai thừa)
Ngoài việc sử dụng đệ quy để tính số Fibonacci thứ N, chúng ta còn hay dùng đệ quy để tính N giai thừa. Việc tính giai thừa chúng ta có thể hoàn toàn thực hiện bằng một vòng for cực kì đơn giản, nhưng khi các bạn sử dụng đệ quy thì trông đoạn code sẽ tường minh hơn rất nhiều.
Như chúng ta đã biết cách tính N! sẽ như sau:
[latex]n! = 1 times 2 times 3 times … times n[/latex]
Ngoài ra trong toán học [latex]0! = 1! = 1[/latex] việc định nghĩa này giúp chúng ta xác định được “phần neo” của hàm đệ quy. Vì vậy, chúng ta sẽ tính ngược lại là:
[latex]n! = n times (n-1) times (n-2) times … times 3 times 2 times 1[/latex]
Từ đó chúng ta suy ra được:
[latex]n! = n times (n-1)![/latex]
Sau khi chúng ta đã có hết tất cả phần neo, và công thức truy hồi chúng ta dễ dàng viết được hàm tính [latex]n![/latex] bằng đệ quy như sau:
int frac(int n) {
if (n <= 1)
return 1;
return n * frac(n - 1);
}Các bạn có thể sử dụng hàm tính giai thừa này chẳng hạn muốn tính [latex]9![/latex] các bạn sử dụng frac(9). Và sau khi cho ra đáp án các bạn có thể kiểm tra lại tính đúng đắn của hàm trên bằng cách so sánh kết quả với kết quả của các máy tính cầm tay hoặc những phương tiện hỗ trợ tính toán khác.
Tổng kết
Như vậy là trong bài học ngày hôm này mình đã trình bày cho các bạn về hàm đệ quy, định nghĩa cũng như là các ví dụ đơn giản. Trong bài học tiếp theo mình sẽ trình bày về, phạm vi của biến trong C# đây sẽ là một phần khá thú vị và có nhiều ứng dụng trong việc lập trình thực tế sau này. Cảm ơn các bạn đã đọc bài viết. Hãy tiếp tục ủng hộ Lập trình không khó trong các bài viết tiếp theo nhé !
(ngoài ra các bạn có thể thử sức với một số bài tập sau đây)



Trả lời