Mình vừa bước vào học môn đồ họa máy tính với ngôn ngữ c/c++ và tìm tòi được một số thông tin về áp dụng thuật toán Breshenham để vẽ đường thẳng nên trong bài viết hôm nay mình xin chia sẻ cho các bạn
Thuật toán Breshenham
Cho 2 điểm A(x1,y1) B(x2, y2), nhiệm vụ của chúng ta là áp dụng thuật toán Breshenham để vễ đoạn thẳng AB.
Xây dựng phương trình đường thẳng theo thuật toán Breshenham có dạng:
Trường hợp hệ số góc 0 < m <= 1:
P = 2dy – dx
nếu P >= 0 y++; P = P + (2dy – 2dx);
còn lại P = P + 2dy;
Thuật toán Bresenham vẽ đoạn thẳng trường cho trường hợp hệ số góc 0<m<1 có thể mô tả tóm tắt như sau:
- Bước 1:
- Tính Dx = |x2 – x1| , Dy = |y2 – y1| và p = 2Dy – Dx.
- Chọn điểm xuất phát (x,y) = (x1,y1).
- Vẽ điểm (x,y).
- Bước 2: Nếu x<x2 thì x = x+1.
- Nếu p < 0: p = p + 2Dy
Ngược lại: p = p + 2( Dy – Dx) và y = y+1.
- Vẽ điểm (x,y) mới.
- Bước 3: Lặp lại bước 2 cho đến khi x = x2.
Code minh họa:
#include <graphics.h>
int color = RED;
void Bresenham(int x1, int y1, int x2, int y2){
int x, y, Dx, Dy, p;
Dx = abs(x2 - x1);
Dy = abs(y2 - y1);
p = 2*Dy - Dx;
x = x1;
y = y1;
putpixel(x,y,color);
while(x != x2){
delay(10);
if (p<0) p += 2*Dy;
else{
p += 2*(Dy-Dx);
y ++;
}
x ++;
putpixel(x, y, color);
}
}
int main(){
int gd,gm=VGA; gd=DETECT;
initgraph(&gd,&gm,NULL);
setbkcolor(WHITE);
Bresenham(50,150, 300, 200); // ve duong thang
getchar();
return 0;
}
Trường hợp hệ số góc -1<= m < 0:
P = 2dy + dx
nếu P < 0 thì y–; P = P + (2dy + 2dx);
còn lại P = P + 2dy;
Trường hợp hệ số góc m > 1:
P = 2dx – dy
nếu P >=0 thì x++; P = P + (2dx – 2dy);
còn lại P = P + 2dx;
Trường hợp hệ số góc nhỏ m > -1:
P = 2dx + dy
nếu P < 0 thì x–; P = P+ (2dx + 2dy);
còn lại P = P + 2dx;
Ngoài ra còn có 2 trường hợp vẽ đường thẳng đứng và đường ngang, khá là dễ nên mình không nhắc tới ở đây.
Code đầy đủ:
# sử dụng thuật toán Breshenham để vẽ đường thẳng
#include <graphics.h>
int colorRedBlue = BLUE;
void lineBresenham(int x1, int y1, int x2, int y2){
int x, y, Dx, Dy, p;
Dx = abs(x2 - x1);
Dy = abs(y2 - y1);
p = 2*Dy - Dx;
x = x1;
y = y1;
int x_unit = 1, y_unit = 1;
#xét trường hợp để cho y_unit và x_unit để vẽ tăng lên hay giảm xuống
if (x2 - x1 < 0)
x_unit = -x_unit;
if (y2 - y1 < 0)
y_unit = -y_unit;
if (x1 == x2) // trường hợp vẽ đường thẳng đứng
{
while (y != y2+1)
{
delay(10);
y += y_unit;
putpixel(x, y, colorRedBlue);
}
}
else if (y1 == y2) // trường hợp vẽ đường ngang
{
while (x != x2+1)
{
delay(10);
x += x_unit;
putpixel(x, y, colorRedBlue);
}
}
// trường hợp vẽ các đường xiên
else{
putpixel(x, y, colorRedBlue);
while(x != x2){
delay(10);
if (p<0) p += 2*Dy;
else{
p += 2*(Dy-Dx);
y += y_unit;
}
x += x_unit;
putpixel(x, y, colorRedBlue);
}
}
}
int main(){
int gd,gm=VGA; gd=DETECT;
initgraph(&gd,&gm,NULL);
setbkcolor(WHITE);
lineBresenham(200,200,50,60);
lineBresenham(200,200,50,200);
lineBresenham(200,200,50,300);
lineBresenham(200,200,200,400);
lineBresenham(200,200,300,400);
lineBresenham(200,200,300,200);
lineBresenham(200,200,400,60);
lineBresenham(200,200,200,60);
getchar();
return 0;
}
Kết quả:
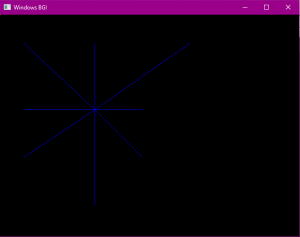
Theo dõi lập trình không khó tại:



Để lại một bình luận